Laminar and Turbulent Flow

Laminar and Turbulent Flow

The characteristics of laminar and turbulent flow are very different. To understand why turbulent or laminar flow is desirable in the operation of a particular system, it is necessary to understand the characteristics of laminar and turbulent flow.

Flow Regimes

All fluid flow is classified into one of two broad categories or regimes. These two flow regimes are laminar flow and turbulent flow. The flow regime, whether laminar or turbulent, is important in the design and operation of any fluid system. The amount of fluid friction, which determines the amount of energy required to maintain the desired flow, depends upon the mode of flow. This is also an important consideration in certain applications that involve heat transfer to the fluid.

Laminar Flow

Laminar flow is also referred to as streamline or viscous flow. These terms are descriptive of the flow because, in laminar flow, (1) layers of water flowing over one another at different speeds with virtually no mixing between layers, (2) fluid particles move in definite and observable paths or streamlines, and (3) the flow is characteristic of viscous (thick) fluid or is one in which viscosity of the fluid plays a significant part.

Turbulent Flow

Turbulent flow is characterized by the irregular movement of particles of the fluid. There is no definite frequency as there is in wave motion. The particles travel in irregular paths with no observable pattern and no definite layers.

Flow Velocity Profiles

Not all fluid particles travel at the same velocity within a pipe. The shape of the velocity curve (the velocity profile across any given section of the pipe) depends upon whether the flow is laminar or turbulent. If the flow in a pipe is laminar, the velocity distribution at a cross section will be parabolic in shape with the maximum velocity at the center being about twice the average velocity in the pipe. In turbulent flow, a fairly flat velocity distribution exists across the section of pipe, with the result that the entire fluid flows at a given single value. Figure 5 helps illustrate the above ideas. The velocity of the fluid in contact with the pipe wall is essentially zero and increases the further away from the wall.

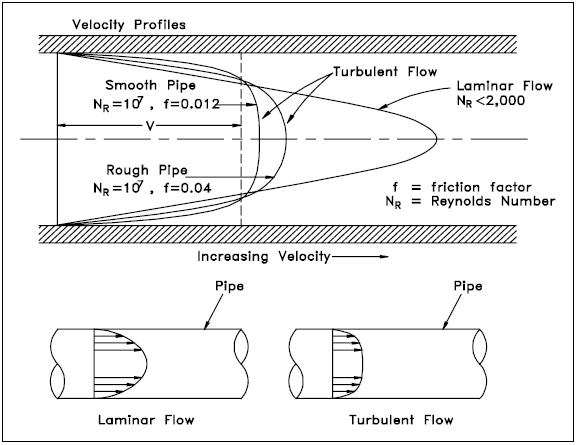
Note from Figure 5 that the velocity profile depends upon the surface condition of the pipe wall. A smoother wall results in a more uniform velocity profile than a rough pipe wall.

Average (Bulk) Velocity

In many fluid flow problems, instead of determining exact velocities at different locations in the same flow cross-section, it is sufficient to allow a single average velocity to represent the velocity of all fluid at that point in the pipe. This is fairly simple for turbulent flow since the velocity profile is flat over the majority of the pipe cross-section. It is reasonable to assume that the average velocity is the same as the velocity at the center of the pipe.

If the flow regime is laminar (the velocity profile is parabolic), the problem still exists of trying to represent the "average" velocity at any given cross-section since an average value is used in the fluid flow equations. Technically, this is done by means of integral calculus. Practically, the student should use an average value that is half of the center line value.

Viscosity

Viscosity is a fluid property that measures the resistance of the fluid to deforming due to a shear force. Viscosity is the internal friction of a fluid which makes it resist flowing past a solid surface or other layers of the fluid. Viscosity can also be considered to be a measure of the resistance of a fluid to flowing. A thick oil has a high viscosity; water has a low viscosity. The unit of measurement for absolute viscosity is:

The viscosity of a fluid is usually significantly dependent on the temperature of the fluid and relatively independent of the pressure. For most fluids, as the temperature of the fluid increases, the viscosity of the fluid decreases. An example of this can be seen in the lubricating oil of engines. When the engine and its lubricating oil are cold, the oil is very viscous, or thick. After the engine is started and the lubricating oil increases in temperature, the viscosity of the oil decreases significantly and the oil seems much thinner.

Ideal Fluid

An ideal fluid is one that is incompressible and has no viscosity. Ideal fluids do not actually exist, but sometimes it is useful to consider what would happen to an ideal fluid in a particular fluid flow problem in order to simplify the problem.

Reynolds Number

The flow regime (either laminar or turbulent) is determined by evaluating the Reynolds number of the flow (refer to figure 5). The Reynolds number, based on studies of Osborn Reynolds, is a dimensionless number comprised of the physical characteristics of the flow. Equation 3-7 is used to calculate the Reynolds number (N_R) for fluid flow.

where:

NR	=	Reynolds number (unitless)
v	=	average velocity (ft/sec)
D	=	diameter of pipe (ft)
μ	=	absolute viscosity of fluid (lbf-sec/ft2)
ρ	=	fluid mass density (lbm/ft3)
gc	=	gravitational constant (32.2 ft-lbm/lbf-sec2)

For practical purposes, if the Reynolds number is less than 2000, the flow is laminar. If it is greater than 3500, the flow is turbulent. Flows with Reynolds numbers between 2000 and 3500 are sometimes referred to as transitional flows. Most fluid systems in nuclear facilities operate with turbulent flow. Reynolds numbers can be conveniently determined using a Moody Chart, an example of which is shown below. Additional detail on the use of the Moody Chart is provided in subsequent text.

---

---

---