Bernoulli's Equation

This page provides the chapter on Bernoulli's equation from the "DOE Fundamentals Handbook: Thermodynamics, Heat Transfer, and Fluid Flow," DOE-HDBK-1012/3-92, U.S. Department of Energy, June 1992.

Other related chapters from the "DOE Fundamentals Handbook: Thermodynamics, Heat Transfer, and Fluid Flow" can be seen to the right.

DOE Handbook: Fluid Flow

Bernoulli's Equation

Bernoulli's equation is a special case of the general energy equation that is probably the most widely-used tool for solving fluid flow problems. It provides an easy way to relate the elevation head, velocity head, and pressure head of a fluid. It is possible to modify Bernoulli's equation in a manner that accounts for head losses and pump work.

General Energy Equation

The conservation of energy principle states that energy can be neither created nor destroyed. This is equivalent to the First Law of Thermodynamics, which was used to develop the general energy equation in the module on thermodynamics. Equation 3-8 is a statement of the general energy equation for an open system.

Q + (U + PE + KE + PV)_in = W + (U + PE + KE + PV)_out + (U + PE + KE + PV)_stored

(3-8)

where:

Q	=	heat (Btu)
U	=	internal energy (Btu)
PE	=	potential energy (ft-lbf)
KE	=	kinetic energy (ft-lbf)
P	=	pressure (lbf/ft²)
V	=	volume (ft³)
W	=	work (ft-lbf)

Simplified Bernoulli Equation

Bernoulli's equation results from the application of the general energy equation and the first law of thermodynamics to a steady flow system in which no work is done on or by the fluid, no heat is transferred to or from the fluid, and no change occurs in the internal energy (i.e., no temperature change) of the fluid. Under these conditions, the general energy equation is simplified to Equation 3-9.

(PE + KE + PV)₁ = (PE + KE + PV)₂

(3-9)

Substituting appropriate expressions for the potential energy and kinetic energy, Equation 3-9 can be rewritten as Equation 3-10.

$$ {m g z_1 \over g_c} + {m v_1^2 \over 2 g_c} + P_1 V_1 = {m g z_2 \over g_c} + {m v_2^2 \over 2 g_c} + P_2 V_2 $$

(3-10)

where:

m	=	mass (lbm)
z	=	height above reference (ft)
v	=	average velocity (ft/sec)
g	=	acceleration due to gravity (32.17 ft/sec²)
g_c	=	gravitational constant, (32.17 ft-lbm/lbf-sec²)

Note: The factor g_c is only required when the English System of measurement is used and mass is measured in pound mass. It is essentially a conversion factor needed to allow the units to come out directly. No factor is necessary if mass is measured in slugs or if the metric system of measurement is used.

Each term in Equation 3-10 represents a form of energy possessed by a moving fluid (potential, kinetic, and pressure related energies). In essence, the equation physically represents a balance of the KE, PE, PV energies so that if one form of energy increases, one or more of the others will decrease to compensate and vice versa.

Multiplying all terms in Equation 3-10 by the factor g_c/mg results in the form of Bernoulli's equation shown by Equation 3-11.

$$ z_1 + {v_1^2 \over 2 g} + P_1 \nu_1 {g_c \over g} = z_2 + {v_2^2 \over 2 g} + P_2 \nu_2 {g_c \over g} $$

(3-11)

where:

z	=	height above reference level (ft)
v	=	average velocity of fluid (ft/sec)
P	=	pressure of fluid (lbf/ft²)
ν	=	specific volume of fluid (ft³/lbm)
g	=	acceleration due to gravity (ft/sec²)
g_c	=	gravitational constant, (32.17 ft-lbm/lbf-sec²)

Head

Since the units for all the different forms of energy in Equation 3-11 are measured in units of distance, these terms are sometimes referred to as "heads" (pressure head, velocity head, and elevation head). The term head is used by engineers in reference to pressure. It is a reference to the height, typically in feet, of a column of water that a given pressure will support. Each of the energies possessed by a fluid can be expressed in terms of head. The elevation head represents the potential energy of a fluid due to its elevation above a reference level. The velocity head represents the kinetic energy of the fluid. It is the height in feet that a flowing fluid would rise in a column if all of its kinetic energy were converted to potential energy. The pressure head represents the flow energy of a column of fluid whose weight is equivalent to the pressure of the fluid.

The sum of the elevation head, velocity head, and pressure head of a fluid is called the total head. Thus, Bernoulli's equation states that the total head of the fluid is constant.

Earn Continuing Education Credit for Reading This Page

PDH Classroom offers a continuing education course based on this Bernoulli's equation reference page. This course can be used to fulfill PDH credit requirements for maintaining your PE license.

Now that you've read this reference page, earn credit for it!

View the course now:

View Course

Energy Conversions in Fluid Systems

Bernoulli's equation makes it easy to examine how energy transfers take place among elevation head, velocity head, and pressure head. It is possible to examine individual components of piping systems and determine what fluid properties are varying and how the energy balance is affected.

If a pipe containing an ideal fluid undergoes a gradual expansion in diameter, the continuity equation tells us that as the diameter and flow area get bigger, the flow velocity must decrease to maintain the same mass flow rate. Since the outlet velocity is less than the inlet velocity, the velocity head of the flow must decrease from the inlet to the outlet. If the pipe lies horizontal, there is no change in elevation head; therefore, the decrease in velocity head must be compensated for by an increase in pressure head. Since we are considering an ideal fluid that is incompressible, the specific volume of the fluid will not change. The only way that the pressure head for an incompressible fluid can increase is for the pressure to increase. So the Bernoulli equation indicates that a decrease in flow velocity in a horizontal pipe will result in an increase in pressure.

If a constant diameter pipe containing an ideal fluid undergoes a decrease in elevation, the same net effect results, but for different reasons. In this case the flow velocity and the velocity head must be constant to satisfy the mass continuity equation.

So the decrease in elevation head can only be compensated for by an increase in pressure head. Again, the fluid is incompressible so the increase in pressure head must result in an increase in pressure.

Although the Bernoulli equation has several restrictions placed upon it, there are many physical fluid problems to which it is applied. As in the case of the conservation of mass, the Bernoulli equation may be applied to problems in which more than one flow may enter or leave the system at the same time. Of particular note is the fact that series and parallel piping system problems are solved using the Bernoulli equation.

Example: Bernoulli's Equation

Assume frictionless flow in a long, horizontal, conical pipe. The diameter is 2.0 ft at one end and 4.0 ft at the other. The pressure head at the smaller end is 16 ft of water. If water flows through this cone at a rate of 125.6 ft³/sec, find the velocities at the two ends and the pressure head at the larger end.

Solution:

$$ \dot{V}_1 = A_1 v_1 $$ $$ v_1 = {\dot{V}_1 \over A_1} $$ $$ v_1 = { 125.6 ~{\text{ft}^3 \over \text{sec}} \over \pi ~(1 ~\text{ft})^2 } $$ $$ v_1 = 40 ~{\text{ft} \over \text{sec}} $$

$$ \dot{V}_2 = A_2 v_2 $$ $$ v_2 = {\dot{V}_2 \over A_2} $$ $$ v_2 = { 125.6 ~{\text{ft}^3 \over \text{sec}} \over \pi ~(2 ~\text{ft})^2 } $$ $$ v_2 = 10 ~{\text{ft} \over \text{sec}} $$

$$ z_1 + {v_1^2 \over 2 g} + P_1 \nu_1 {g_c \over g} = z_2 + {v_2^2 \over 2 g} + P_2 \nu_2 {g_c \over g} $$ $$ \begin{eqnarray} P_2 \nu_2 {g_c \over g} &=& P_1 \nu_1 {g_c \over g} + (z_1 - z_2) + { v_1^2 - v_2^2 \over 2g } \nonumber \\ &=& 16 ~\text{ft} + 0 ~\text{ft} + { \left({ 40 ~{\text{ft} \over \text{sec}} }\right)^2 - \left({ 10 ~{\text{ft} \over \text{sec}} }\right)^2 \over 2 \left({ 32.17 ~{\text{ft-lbm} \over \text{lbf-sec}^2} }\right) } \nonumber \\ &=& 39.3 ~\text{ft} \end{eqnarray} $$

Restrictions on the Simplified Bernoulli Equation

Practical applications of the simplified Bernoulli Equation to real piping systems is not possible due to two restrictions. One serious restriction of the Bernoulli equation in its present form is that no fluid friction is allowed in solving piping problems. Therefore, Equation 3-10 only applies to ideal fluids. However, in reality, the total head possessed by the fluid cannot be transferred completely from one point to another because of friction. Taking these losses of head into account would provide a much more accurate description of what takes place physically. This is especially true because one purpose of a pump in a fluid system is to overcome the losses in pressure due to pipe friction.

The second restriction on Bernoulli's equation is that no work is allowed to be done on or by the fluid. This restriction prevents two points in a fluid stream from being analyzed if a pump exists between the two points. Since most flow systems include pumps, this is a significant limitation. Fortunately, the simplified Bernoulli equation can be modified in a manner that satisfactorily deals with both head losses and pump work.

Extended Bernoulli

The Bernoulli equation can be modified to take into account gains and losses of head. The resulting equation, referred to as the Extended Bernoulli equation, is very useful in solving most fluid flow problems. In fact, the Extended Bernoulli equation is probably used more than any other fluid flow equation. Equation 3-12 is one form of the Extended Bernoulli equation.

$$ z_1 + {v_1^2 \over 2 g} + P_1 \nu_1 {g_c \over g} + H_p = z_2 + {v_2^2 \over 2 g} + P_2 \nu_2 {g_c \over g} + H_f $$

(3-12)

where:

z	=	height above reference level (ft)
v	=	average velocity of fluid (ft/sec)
P	=	pressure of fluid (lbf/ft²)
ν	=	specific volume of fluid (ft³/lbm)
H_p	=	head added by pump (ft)
H_f	=	head loss due to fluid friction (ft)
g	=	acceleration due to gravity (ft/sec²)
g_c	=	gravitational constant, (32.17 ft-lbm/lbf-sec²)

The head loss due to fluid friction (H_f) represents the energy used in overcoming friction caused by the walls of the pipe. Although it represents a loss of energy from the standpoint of fluid flow, it does not normally represent a significant loss of total energy of the fluid. It also does not violate the law of conservation of energy since the head loss due to friction results in an equivalent increase in the internal energy (u) of the fluid. These losses are greatest as the fluid flows through entrances, exits, pumps, valves, fittings, and any other piping with rough inner surfaces.

Most techniques for evaluating head loss due to friction are empirical (based almost exclusively on experimental evidence) and are based on a proportionality constant called the friction factor (f), which will be discussed in the next section.

Example: Extended Bernoulli

Water is pumped from a large reservoir to a point 65 feet higher than the reservoir. How many feet of head must be added by the pump if 8000 lbm/hr flows through a 6-inch pipe and the frictional head loss is 2 feet? The density of the fluid is 62.4 lbm/ft³, and the cross-sectional area of a 6-inch pipe is 0.2006 ft².

Solution:

To use the modified form of Bernoulli's equation, reference points are chosen at the surface of the reservoir (point 1) and at the outlet of the pipe (point 2). The pressure at the surface of the reservoir is the same as the pressure at the exit of the pipe, i.e., atmospheric pressure. The velocity at point 1 will be essentially zero.

Using the equation for the mass flow rate to determine the velocity at point 2:

$$ \dot{m}_2 = \rho A_2 v_2 $$ $$ v_2 = { \dot{m}_2 \over \rho A_2 } $$ $$ v_2 = { 8000 ~{\text{lbm} \over \text{hr}} \over \left(62.4 ~{\text{lbm} \over \text{ft}^3}\right) (0.2006 ~\text{ft}^2) } $$ $$ v_2 = 639 ~{\text{ft} \over \text{hr}} \left({ 1 ~\text{hr} \over 3600 ~\text{sec} }\right) $$ $$ v_2 = 0.178 ~{\text{ft} \over \text{sec}} $$

Now we can use the Extended Bernoulli equation to determine the required pump head.

$$ z_1 + {v_1^2 \over 2 g} + P_1 \nu_1 {g_c \over g} + H_p = z_2 + {v_2^2 \over 2 g} + P_2 \nu_2 {g_c \over g} + H_f $$

$$ H_p = (z_2 - z_1) + \left({ v_2^2 - v_1^2 \over 2 g }\right) + (P_2 - P_1) ~\nu ~{g_c \over g} + H_f $$

$$ \begin{eqnarray} H_p &=& (z_2 - z_1) + \left({ v_2^2 - v_1^2 \over 2 g }\right) + (P_2 - P_1) ~\nu ~{g_c \over g} + H_f \nonumber \\ &=& 65 ~\text{ft} + { \left({ 0.178 ~{\text{ft} \over \text{sec}} }\right)^2 - \left({ 0 ~{\text{ft} \over \text{sec}} }\right)^2 \over 2 \left({ 32.17 ~{\text{ft-lbm} \over \text{lbf-sec}^2} }\right) } + 0 ~\text{ft} + 2 ~\text{ft} \nonumber \\ H_p &=& 67 ~\text{ft} \end{eqnarray} $$

The student should note that the solution of this example problem has a numerical value that "makes sense" from the data given in the problem. The total head increase of 67 ft. is due primarily to the 65 ft. evaluation increase and the 2 ft. of friction head.

Application of Bernoulli's Equation to a Venturi

Many plant components, such as a venturi, may be analyzed using Bernoulli's equation and the continuity equation. A venturi is a flow measuring device that consists of a gradual contraction followed by a gradual expansion. An example of a venturi is shown in Figure 6. By measuring the differential pressure between the inlet of the venturi (point 1) and the throat of the venturi (point 2), the flow velocity and mass flow rate can be determined based on Bernoulli's equation.

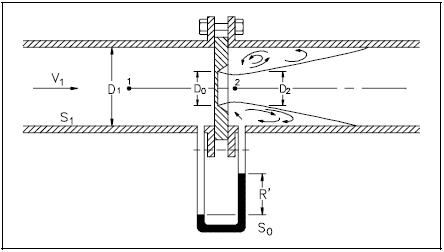
Bernoulli's equation states that the total head of the flow must be constant. Since the elevation does not change significantly, if at all, between points 1 and 2, the elevation head at the two points will be essentially the same and will cancel out of the equation. So Bernoulli's equation simplifies to Equation 3-13 for a venturi.

$$ {v_1^2 \over 2 g} + P_1 \nu_1 {g_c \over g} = {v_2^2 \over 2 g} + P_2 \nu_2 {g_c \over g} $$

(3-13)

Applying the continuity equation to points 1 and 2 allows us to express the flow velocity at point 1 as a function of the flow velocity at point 2 and the ratio of the two flow areas.

$$ \rho_1 A_1 v_1 = \rho_2 A_2 v_2 $$ $$ v_1 = { \rho_2 A_2 v_2 \over \rho_1 A_1 } $$ $$ v_1 = v_2 ~{A_2 \over A_1} $$

Using algebra to rearrange Equation 3-13 and substituting the above result for v₁ allows us to solve for v₂.

$$ {v_2^2 - v_1^2 \over 2g} = (P_1 - P_2) ~\nu ~{g_c \over g} $$ $$ v_2^2 - \left(v_2 ~{A_2 \over A_1}\right)^2 = (P_1 - P_2) ~2 \nu g_c $$ $$ v_2^2 \left[ 1 - \left({A_2 \over A_1}\right)^2 \right] = (P_1 - P_2) ~2 \nu g_c $$ $$ v_2 = \sqrt{ (P_1 - P_2) ~2 \nu g_c \over 1 - \left({A_2 \over A_1}\right)^2 } $$ $$ v_2 = \sqrt{P_1 - P_2} \sqrt{ 2 \nu g_c \over 1 - \left({A_2 \over A_1}\right)^2 } $$

Therefore the flow velocity at the throat of the venturi and the volumetric flow rate are directly proportional to the square root of the differential pressure.

The pressures at the upstream section and throat are actual pressures, and velocities from Bernoulli's equation without a loss term are theoretical velocities. When losses are considered in the energy equation, the velocities are actual velocities. First, with the Bernoulli equation (that is, without a head-loss term), the theoretical velocity at the throat is obtained. Then by multiplying this by the venturi factor (C_v), which accounts for friction losses and equals 0.98 for most venturis, the actual velocity is obtained. The actual velocity times the actual area of the throat determines the actual discharge volumetric flow rate.

The pressure drop, P₁ − P₂, across the venturi can be used to measure the flow rate using a U-tube manometer as shown in Figure 6. The reading, R', of the manometer is proportional to the pressure drop and thus the velocity of the fluid.

Earn Continuing Education Credit for Reading This Page

PDH Classroom offers a continuing education course based on this Bernoulli's equation reference page. This course can be used to fulfill PDH credit requirements for maintaining your PE license.

Now that you've read this reference page, earn credit for it!

View the course now:

View Course

⟸ Previous Page

Next Page ⟹