Air Force Stress Manual:
Pressure Vessels
  1. Simple Thin PV's
  2. Stiffened Thin PV's
  3. Thick Pressure Vessels
  4. Anisotropic PV's
Structural Calculators

Check out these structural calculators:  • Beam Analysis   • Bolted Joints   • Lug Analysis  • Column Buckling

Structural Calculators

Thick Pressure Vessels

This page provides the sections on the analysis of thick pressure vessels from the "Stress Analysis Manual," Air Force Flight Dynamics Laboratory, October 1986.

Other related chapters from the Air Force "Stress Analysis Manual" can be seen to the right.

Analysis of Pressure Vessels
  1. Simple Thin Pressure Vessels
  2. Stiffened Thin Pressure Vessels
  3. Thick Pressure Vessels
  4. Anisotropic Pressure Vessels

Nomenclature for Thick Pressure Vessels

a = inside radius of thick sphere or cylinder
b = outside radius of thick sphere or cylinder
Fmer = meridional or axial stress
Fr = radial stress
Frmax = maximum radial stress
Ft = tangential or circumferential stress
Ftmax = maximum circumferential stress
pi = internal pressure
po = external pressure
r = cylindrical or polar coordinate

8.4 Thick Pressure Vessels

If the ratio of the minimum radius of curvature of a wall to its thickness is less than ten, stresses may no longer be considered constant throughout the wall thickness and radial stresses may not be ignored. Thus, the equations for thin-walled pressure vessels that were developed with these assumptions are no longer valid. This section presents solutions for the stresses in thick-walled cylinders and spheres.

Thick vessels, other than cylindrical and spherical ones, have bending stresses even if there are no discontinuities present. The analysis of these stresses is difficult and is not established on a satisfactory basis as yet. Thus, it is best to determine the intensity of the maximum stresses that exist in unconventional designs by strain gauge measurements or other experimental means.

8.4.1 Thick Cylindrical Pressure Vessels

Figure 8-50 shows a cross section of a thick cylindrical pressure vessel of internal radius a and external radius b.

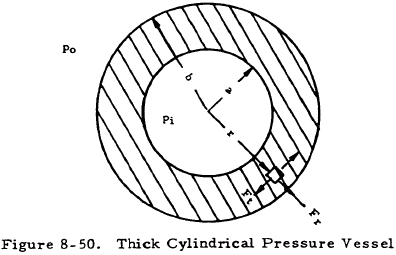
Thick Cylindrical Pressure Vessel

The radial, tangential, and axial stresses, Fr, Ft and Fmer in such a cylinder are given by Equations (8-35), (8-36), and (8-37), respectively.

$$ F_r = { a^2 p_i - b^2 p_o \over b^2 - a^2 } - { a^2 b^2 (p_i - p_o) \over (b^2 - a^2) r^2 } $$
(8-35)
$$ F_t = { a^2 p_i - b^2 p_o \over b^2 - a^2 } + { a^2 b^2 (p_i - p_o) \over (b^2 - a^2) r^2 } $$
(8-36)
$$ F_{mer} = { a^2 p_i - b^2 p_o \over b^2 - a^2 } $$
(8-37)

In order for Equation (8-37) to apply, the point considered must be far enough removed from the ends for St. Venant's principle to apply.

8.4.1.1 Thick Cylindrical Pressure Vessels Under Internal Pressure Only

If po = 0, Equations (8-35) and (8-36) reduce to

$$ F_r = { a^2 p_i \over b^2 - a^2 } \left( 1 - {b^2 \over r^2} \right) $$
(8-38)

and

$$ F_t = { a^2 p_i \over b^2 - a^2 } \left( 1 + {b^2 \over r^2} \right) $$
(8-39)

Both of these stresses have maximum magnitudes at r = a. If the maximum shear stress theory of failure is to be used, the design equation becomes

$$ F_{smax} = { F_{tmax} - F_{rmax} \over 2 } = { b^2 \over b^2 - a^2 } ~p_i $$
(8-40)

8.4.1.2 Thick Cylindrical Pressure Vessels Under External Pressure Only

If pi = 0, Equations (8-35) and (8-36) reduce to

$$ F_r = { -p_o b^2 \over b^2 - a^2 } \left( 1 - {a^2 \over r^2} \right) $$
(8-41)

and

$$ F_t = { -p_o b^2 \over b^2 - a^2 } \left( 1 + {a^2 \over r^2} \right) $$
(8-42)

In this case, both the tangential and radial stresses are always compressive, with the former always the larger of the two. The maximum compressive stress occurs at the inner surface of the cylinder where the radial stress is equal to zero. This maximum compressive stress is given by

$$ F_{tmax} = { -2 b^2 p_o \over b^2 - a^2 } $$
(8-43)

8.4.1.3 Sample Problems - Thick Cylindrical Pressure Vessel

Given: The pressure vessel shown in Figure 8-51.

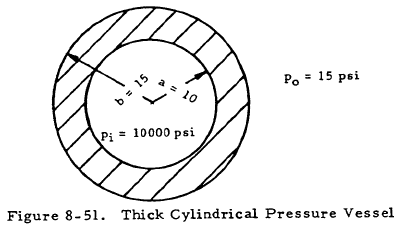
Thick Cylindrical Pressure Vessel

Find: The maximum shear stress in the vessel.

Solution: Assume the external pressure is negligible and apply Equation (8-40). Thus,

$$ F_{smax} = \left({ b^2 \over b^2 - a^2 }\right) p_i = { (15)^2 (10,000) \over [ (15)^2 - (10)^2 ] } = 18,000 ~\text{psi} $$

Need Structural Calculators?

We have a number of structural calculators to choose from. Here are just a few:

Structural Calculators

8.4.2 Thick Spherical Pressure Vessels

The radial and tangential stresses at a distance r from the center of a spherical pressure vessel of inner radius a and outer radius b are given by Equations (8-44) and (8-45).

$$ F_r = { p_o b^3 (r^3 - a^3) \over r^3 (a^3 - b^3) } + { p_i (b^3 - r^3) \over r^3 (a^3 - b^3) } $$
(8-44)
$$ F_t = { p_o b^3 (2 r^3 + a^3) \over 2 r^3 (a^3 - b^3) } - { p_i a^3 (2 r^3 + b^3) \over 2 r^3 (a^3 - b^3) } $$
(8-45)

The terminology here is the same as that shown in Figure 8-50 for cylindrical pressure vessels.

If po = 0,

$$ F_t = { p_i a^3 \over 2 r^2 } { (2 r^3 + b^3) \over b^3 - a^3 } $$
(8-46)

and the greatest tangential tension is at the inner surface at which

$$ F_{tmax} = {p_i \over 2} { 2 a^3 + b^3 \over b^3 - a^3 } $$
(8-47)


⟸ Previous Page
Next Page ⟹