Column Data
This page provides column data applicable to both long and short columns, from the "Stress Analysis Manual," Air Force Flight Dynamics Laboratory, October 1986.
Other related chapters from the Air Force "Stress Analysis Manual" can be seen to the right.
Nomenclature
| A | = | area |
| b | = | linear dimension as indicated in diagrams |
| Fcol | = | maximum fiber stress for primary failure of a column |
| I | = | moment of inertia |
| L | = | length |
| L' | = | effective length = L/√C |
| P | = | axial load |
| Pcr | = | critical load |
| ρ | = | radius of gyration = \( \sqrt{I/A} \) |
2.3.1.1 Column Data Applicable to Both Long and Short Columns
A stable section (not subject to crippling) testing for various lengths will generate data of the form shown in Figure 2-2. The stress Fcol is the stress at failure, and L'/ρ is the ratio of the effective column length to the radius of gyration of the section. This L'/ρ ratio is called the effective slenderness ratio of the column.
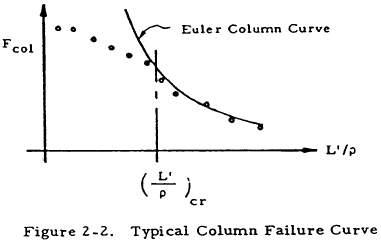
From the figure, it is apparent that the Euler column curve is quite accurate beyond a critical L'/ρ which defines the separation between long and short columns. A great amount of test data, collected for particular materials, is available and eliminates the need to determine whether a long or a short column curve is applicable. A summary of column allowable curves that are applicable to both long and short columns is outlined and presented on the following pages. These curves are based upon the tangent modulus equation which is discussed in Section 2.3.1.11.1. The column allowables are based on minimum guaranteed properties, Basis A, or probability properties, Basis B, if the latter are available. The pertinent basis is indicated in the figures.
| Aluminum Alloys | Figure |
|---|---|
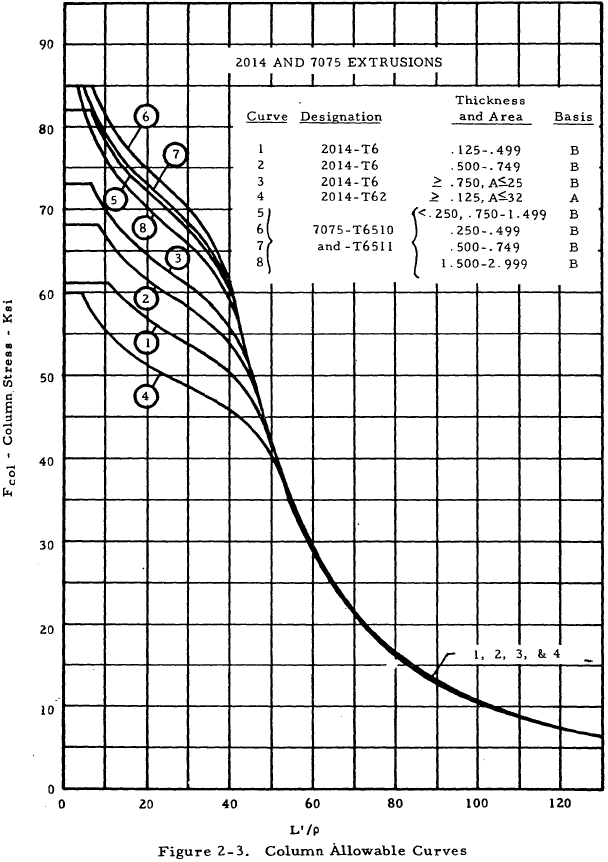
| 2014 Extrusion | 2-3 |
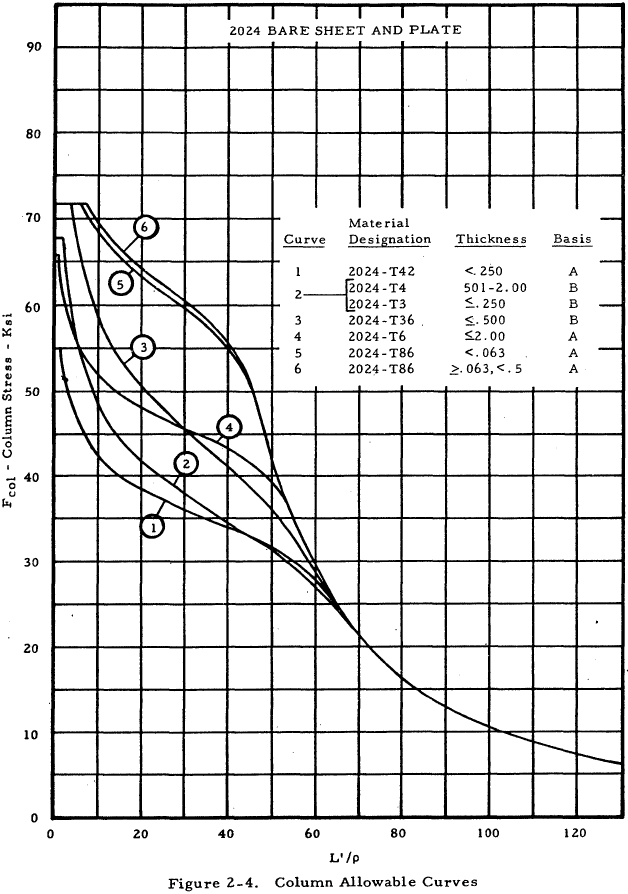
| 2024 Bare Sheet and Plate | 2-4 |
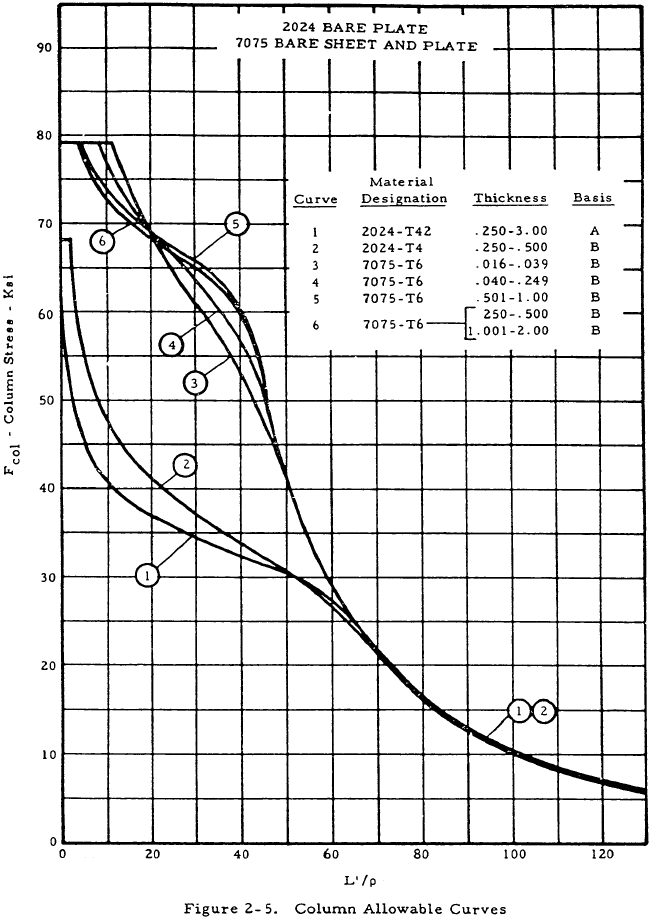
| 2024 Bare Plate | 2-5 |
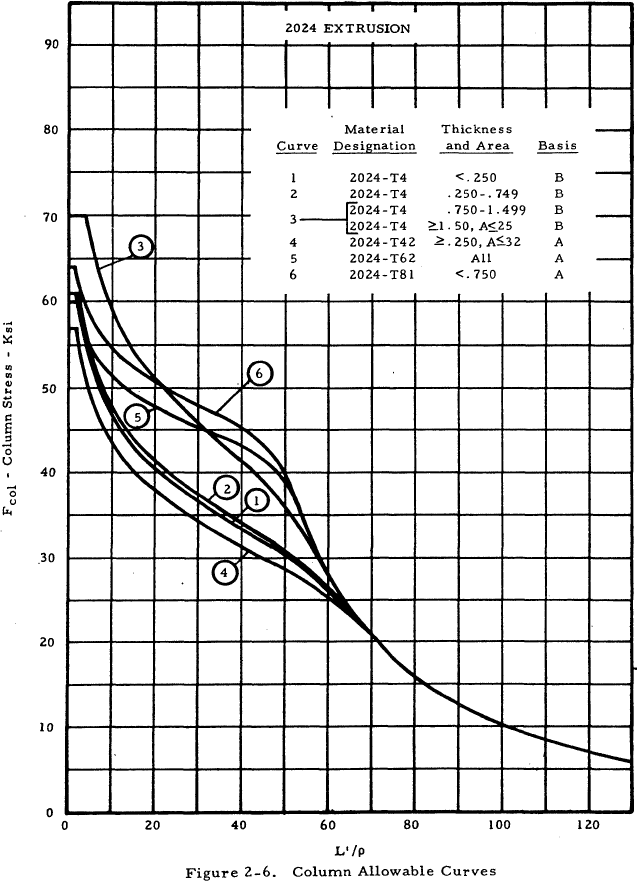
| 2024 Extrusion | 2-6 |
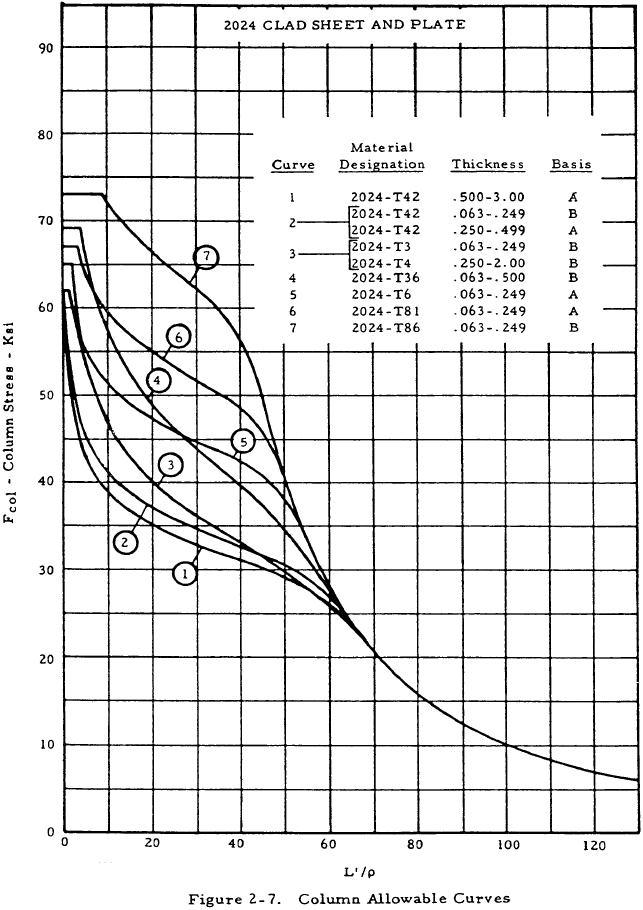
| 2024 Clad Sheet and Plate | 2-7 |
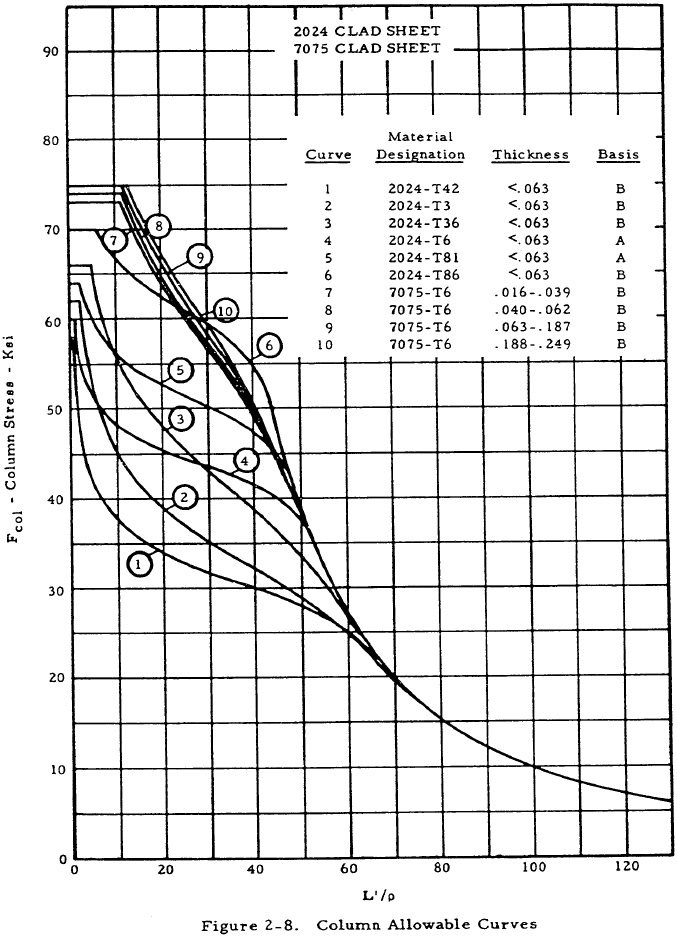
| 2024 Clad Sheet | 2-8 |
| 7075 Bare Sheet and Plate | 2-5 |
| 7075 Extrusions | 2-3 |
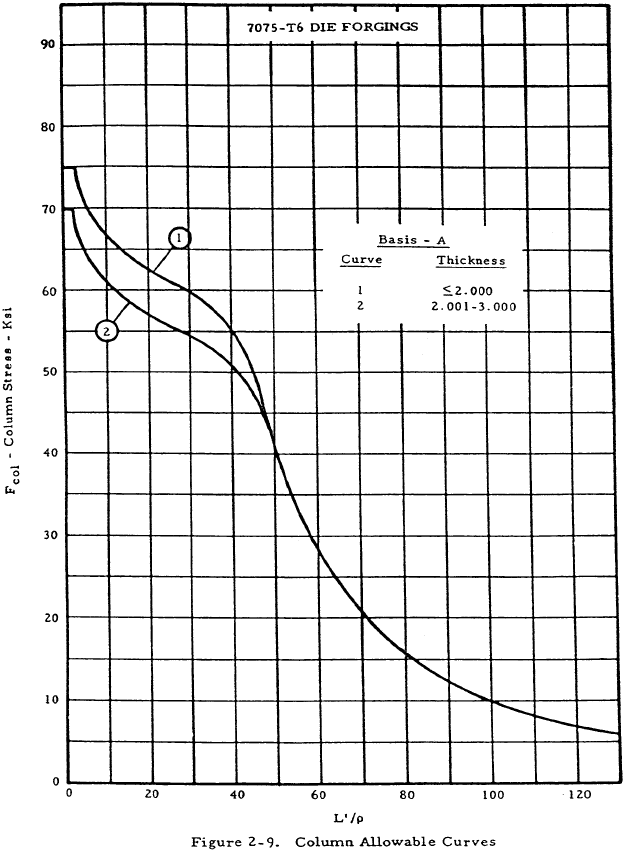
| 7075 Die Forging | 2-9 |
| 7075 Clad Sheet | 2-8 |
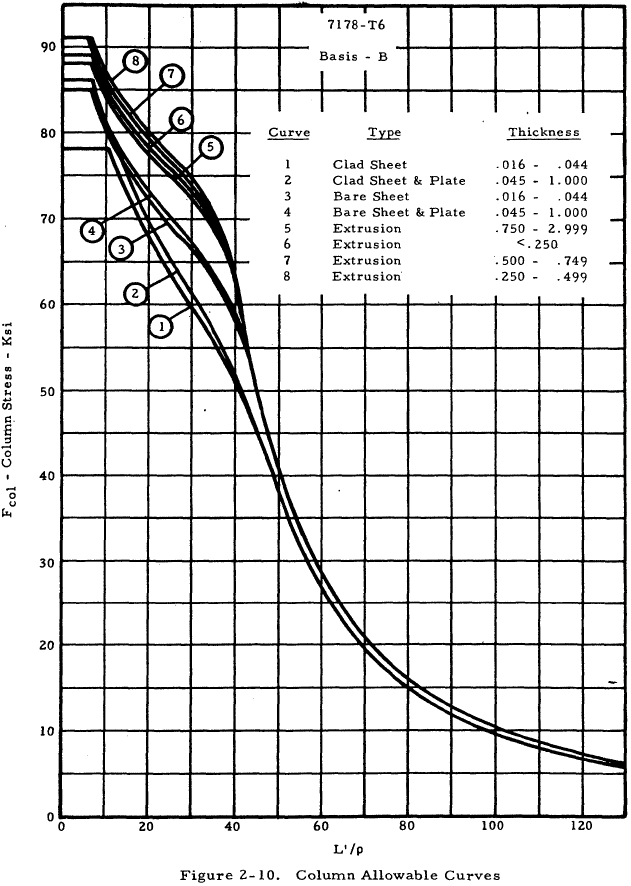
| 7178 Bare Sheet and Plate, Clad Sheet and Plate, and Extrusions | 2-10 |
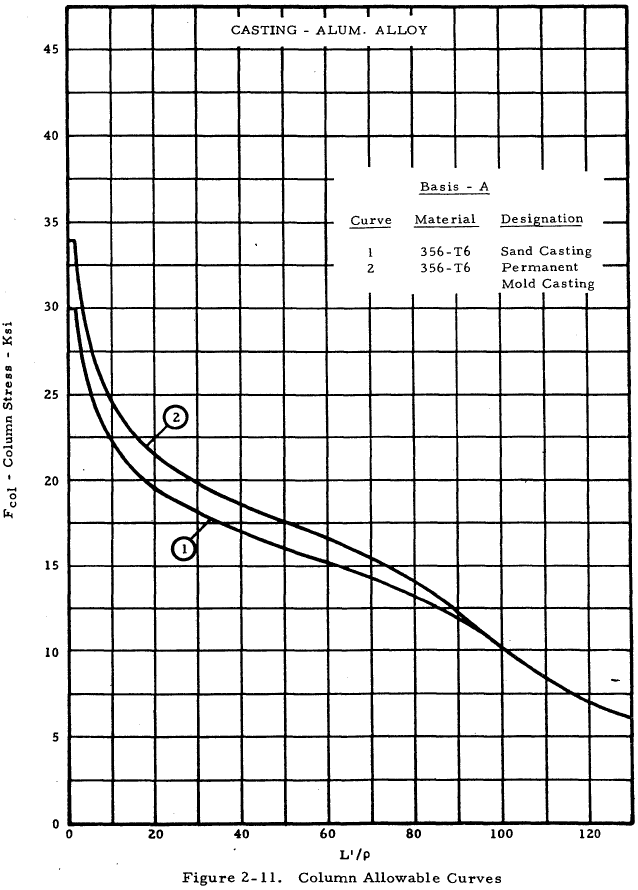
| 356 Casting | 2-11 |
| Magnesium Alloys | Figure |
|---|---|
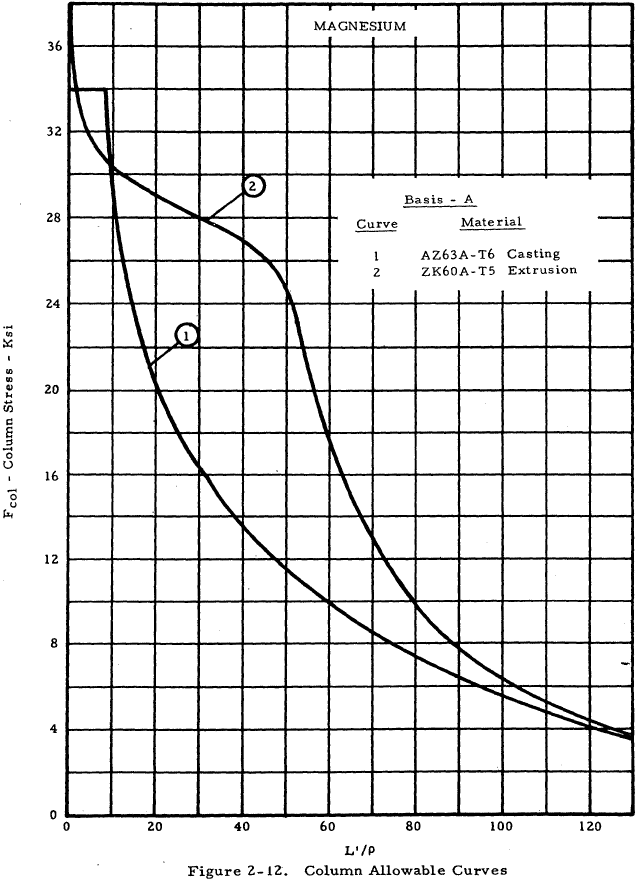
| AZ63A-T6 Casting | 2-12 |
| ZK60A-T5 Extrusion | 2-12 |
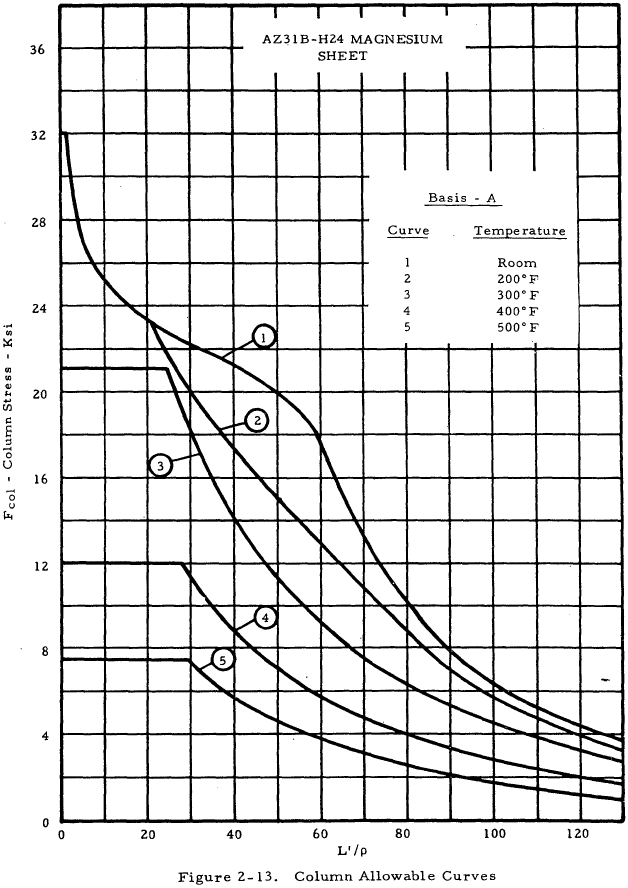
| AZ31B-H24 Sheet | 2-13 |
| HM21A-T8 Sheet | 2-14 |
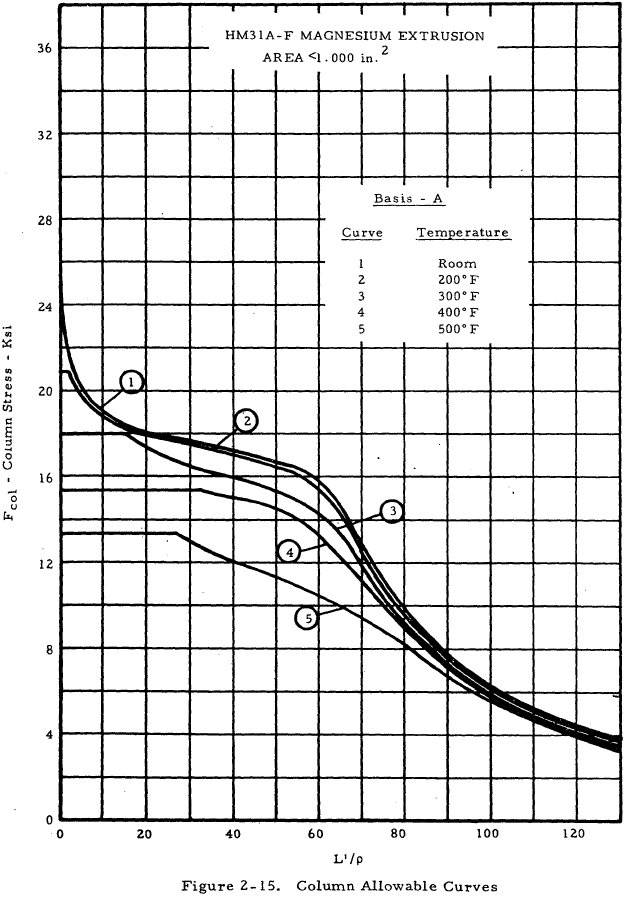
| HM31A-F Extrusion, Area < 1.0 in2 | 2-15 |
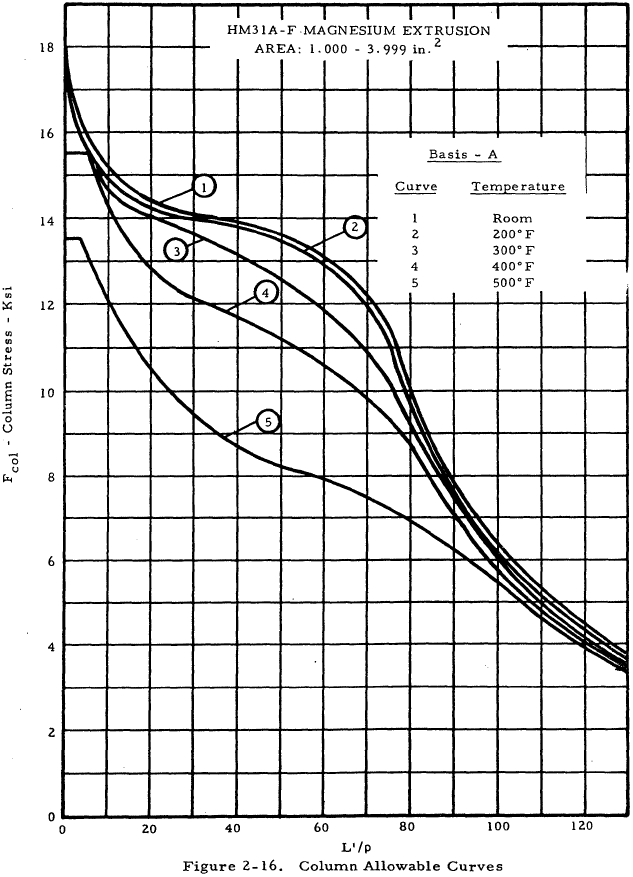
| HM31A-F Extrusion, Area: 1-3.99 in2 | 2-16 |
| Steel Alloys | Figure |
|---|---|
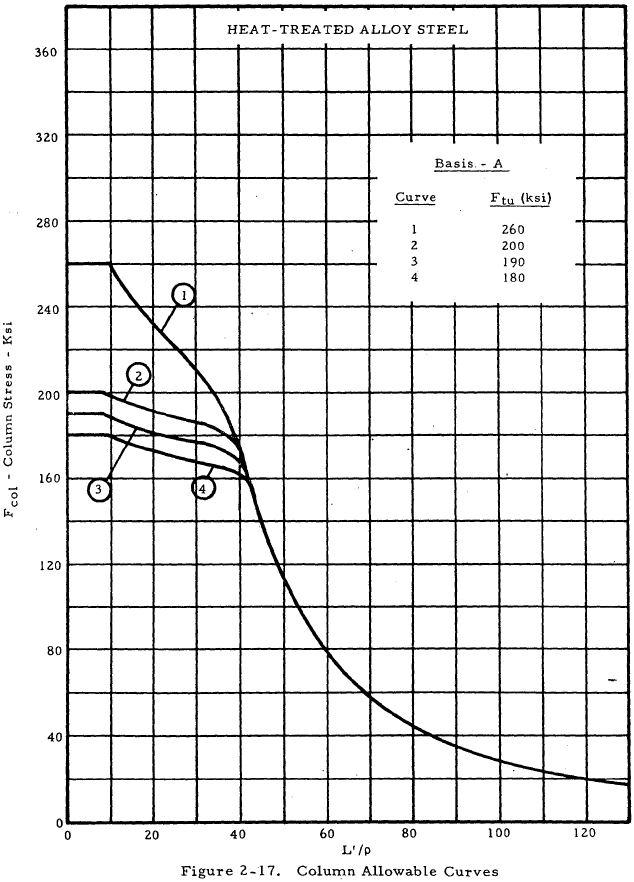
| Heat-treated Ftu = 180-260 ksi | 2-17 |
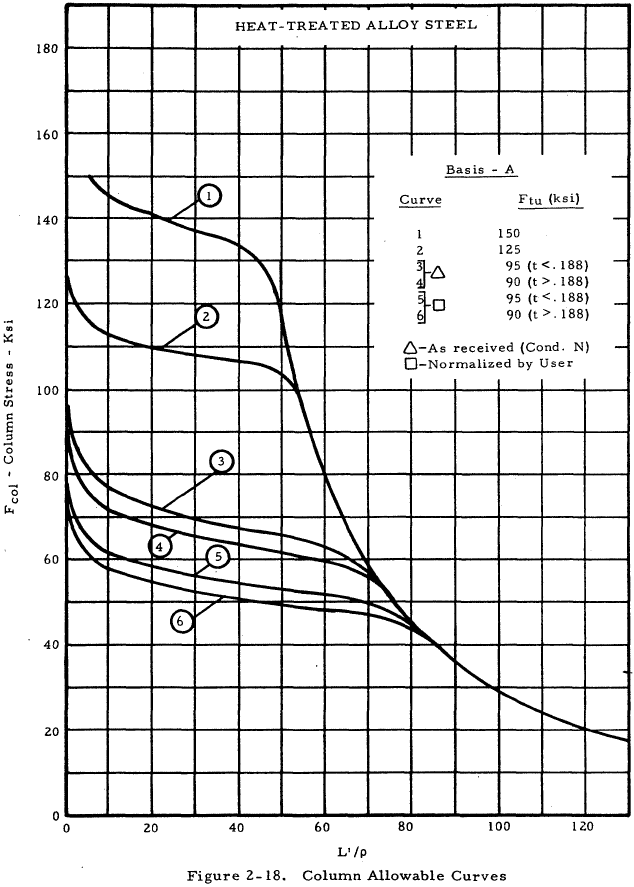
| Heat-treated Ftu = 90-150 ksi | 2-18 |
| Stainless Steel | Figure |
|---|---|
| 18-8 Cold rolled - with grain | 2-19 |
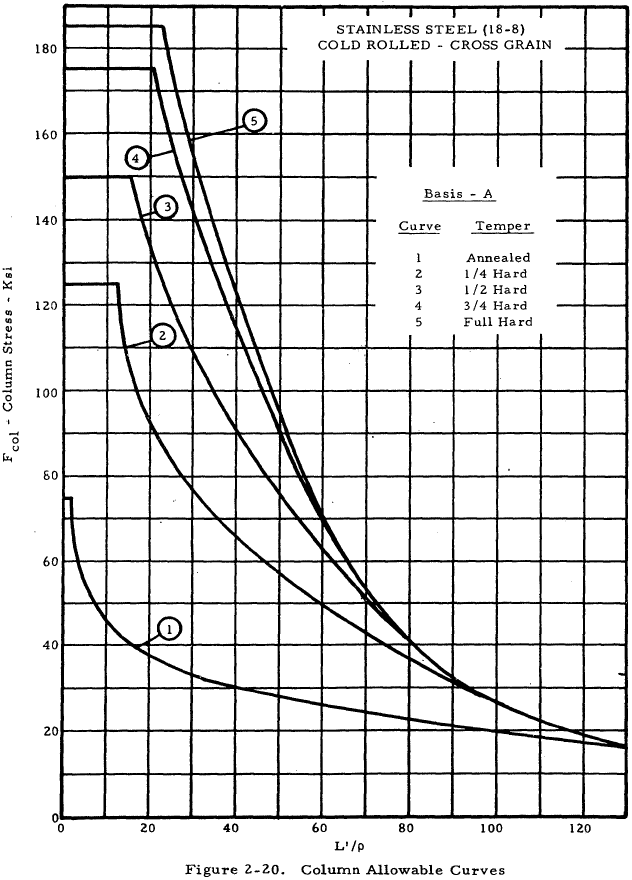
| 18-8 Cold rolled - cross grain | 2-20 |
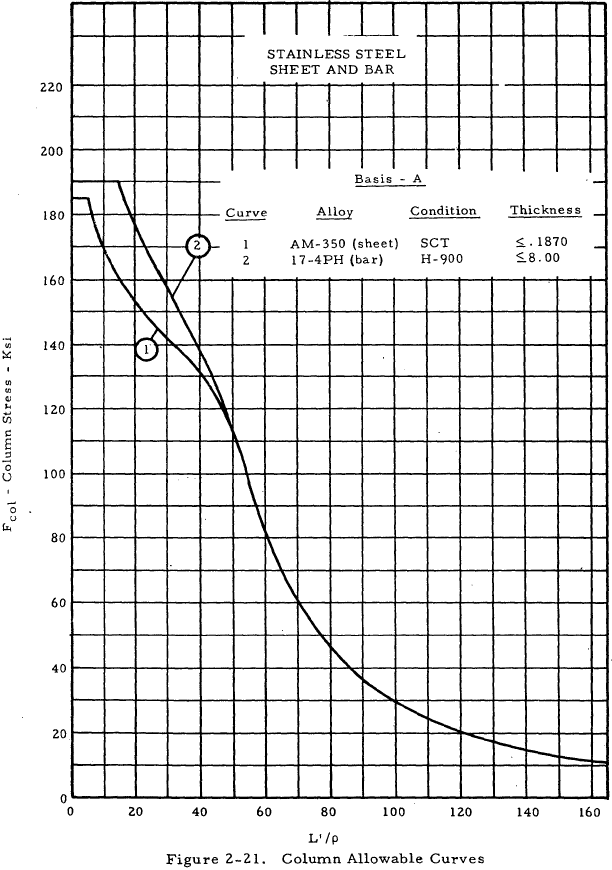
| AM 350 Sheet | 2-21 |
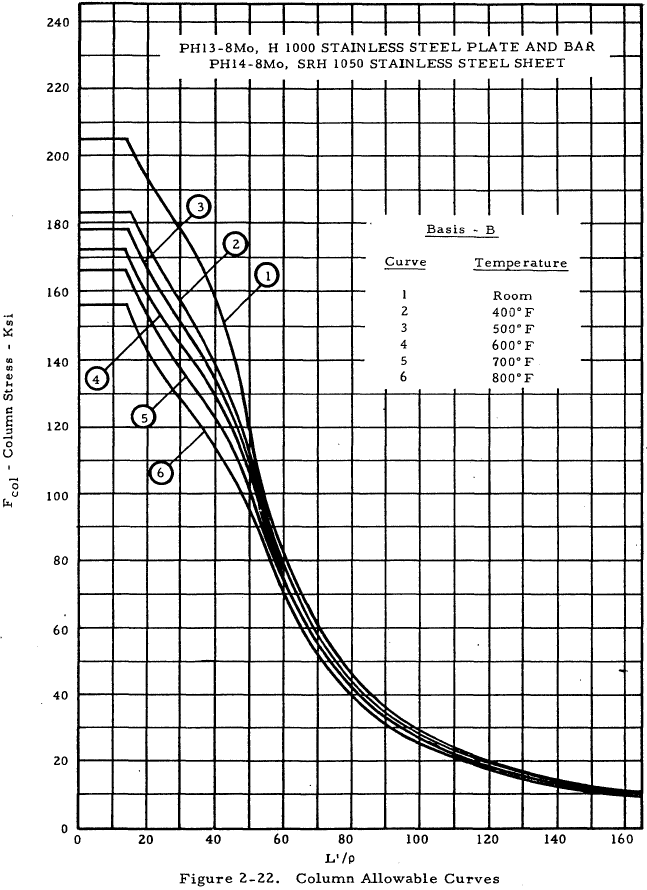
| PH 13-8 Mo Plate and Bar | 2-22 |
| PH 14-8 Mo Sheet | 2-22 |
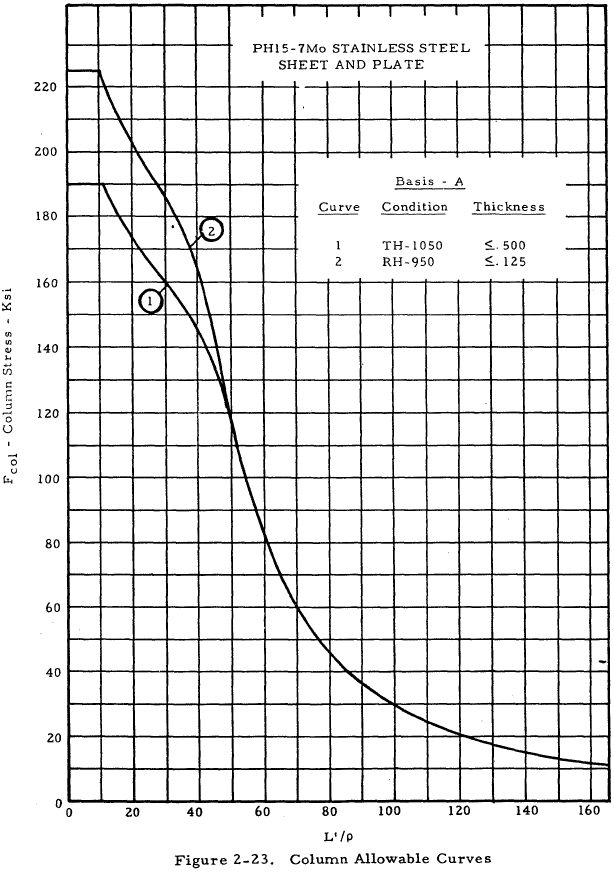
| PH 15-7 Mo Sheet and Plate | 2-23 |
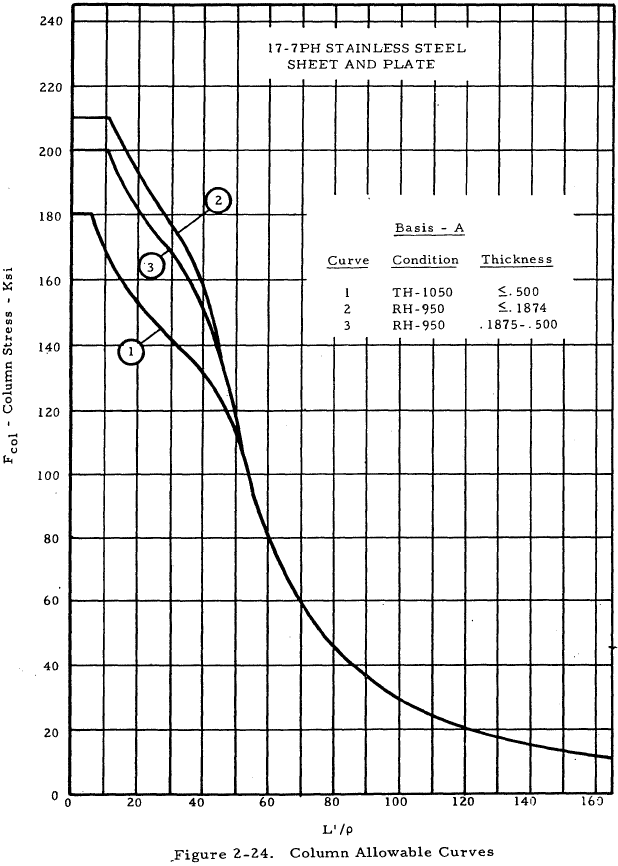
| 17-7 PH Sheet and Plate | 2-24 |
| 17-4 PH Bar | 2-21 |
| Titanium Alloys | Figure |
|---|---|
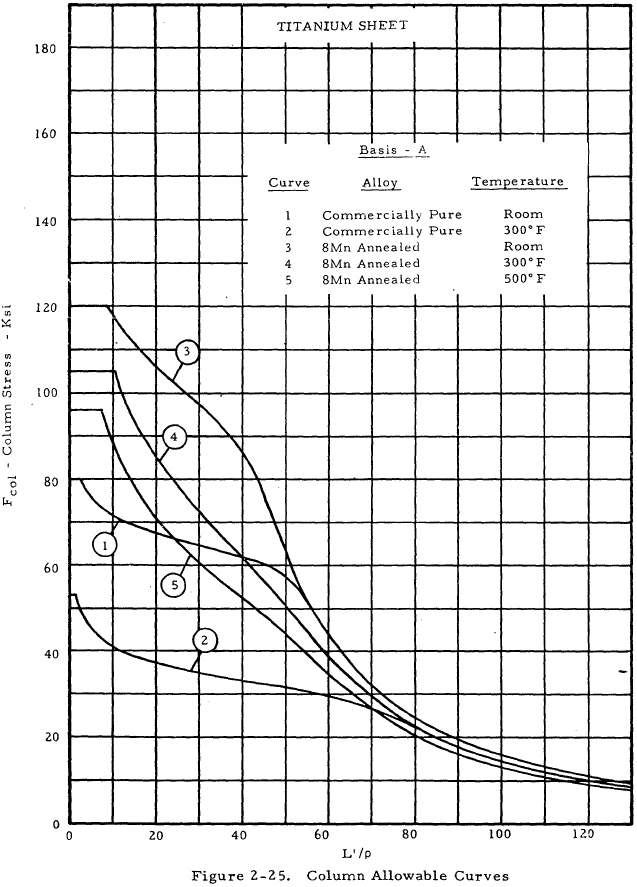
| Commercially Pure Sheet | 2-25 |
| 8 Mn Annealed Sheet | 2-25 |
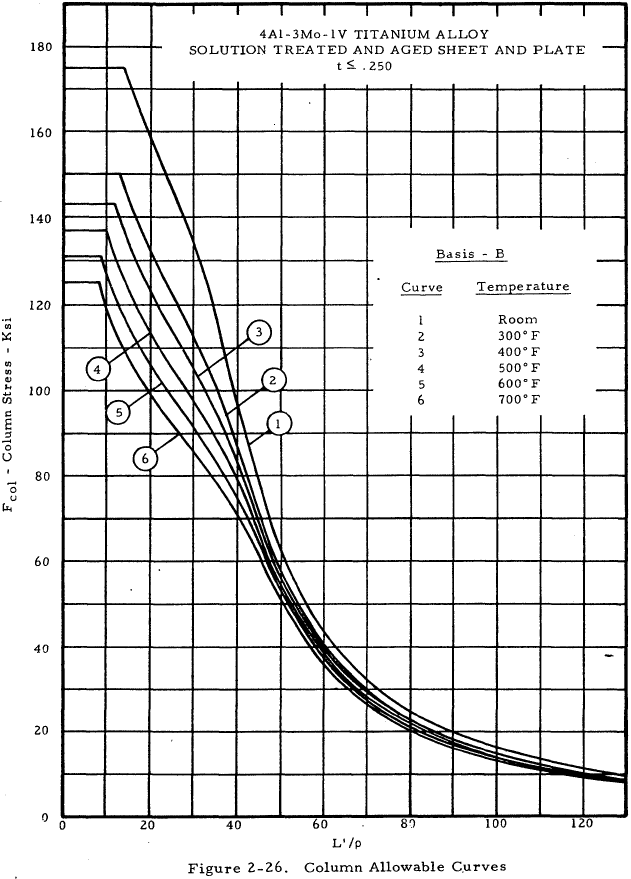
| 4Al-3Mo-1V Solution Treated and Aged Sheet and Plate | 2-26 |
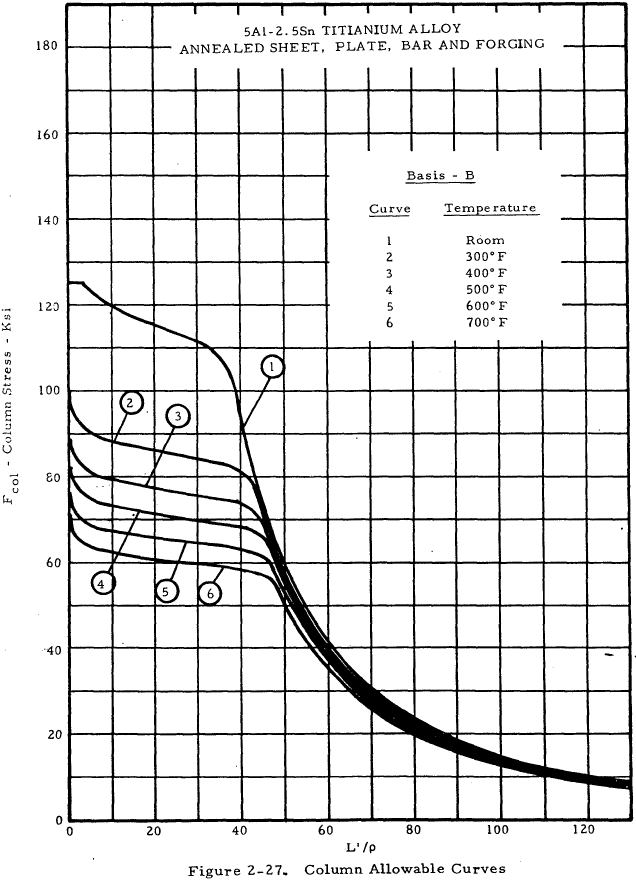
| 5Al-2.5Sn Annealed Sheet, Plate, Bar and Forging | 2-27 |
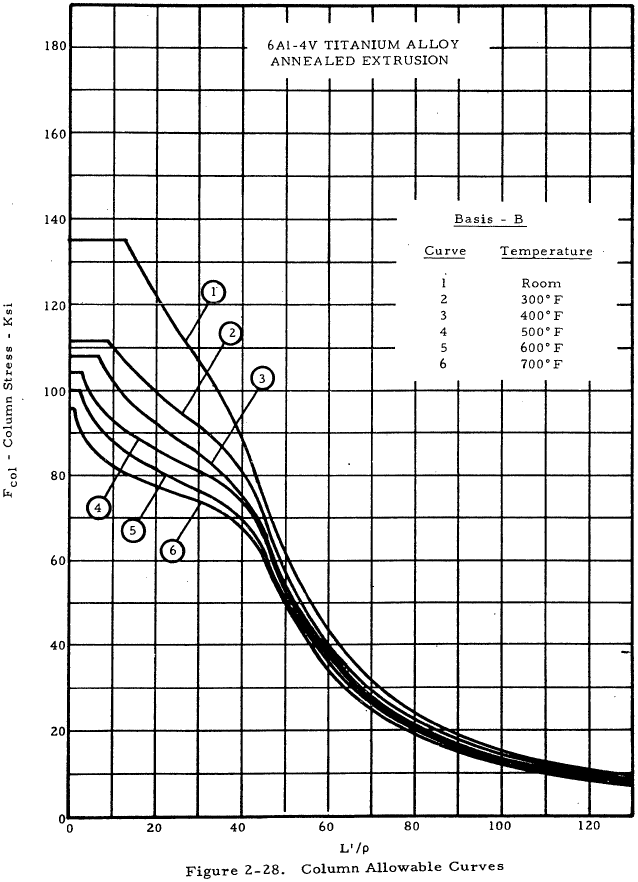
| 6Al-4V Annealed Extrusion | 2-28 |
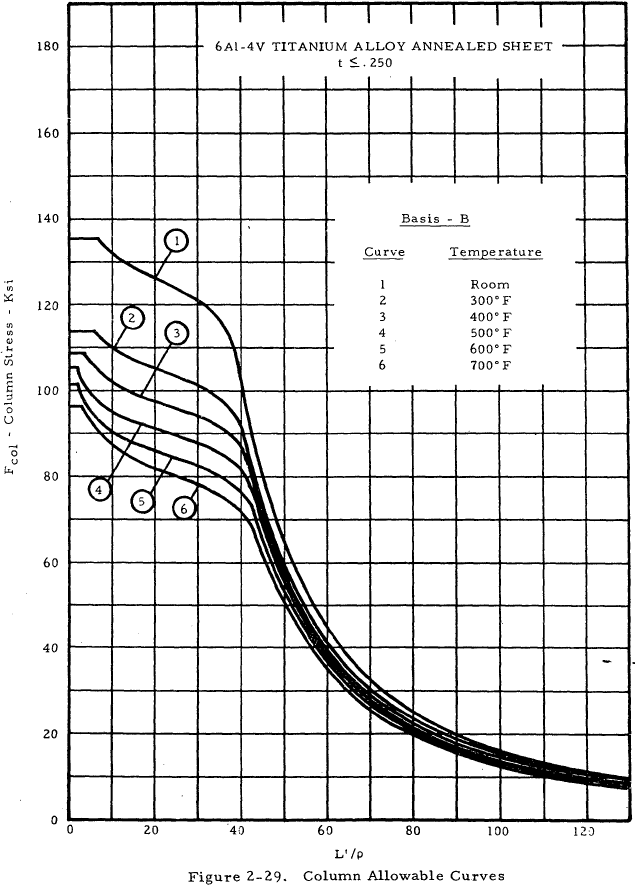
| 6Al-4V Annealed Sheet | 2-29 |
| 6Al-4V Solution Treated and Aged Sheet | 2-30 |
| 6Al-4V Solution Treated and Aged Extrusion | 2-31 |
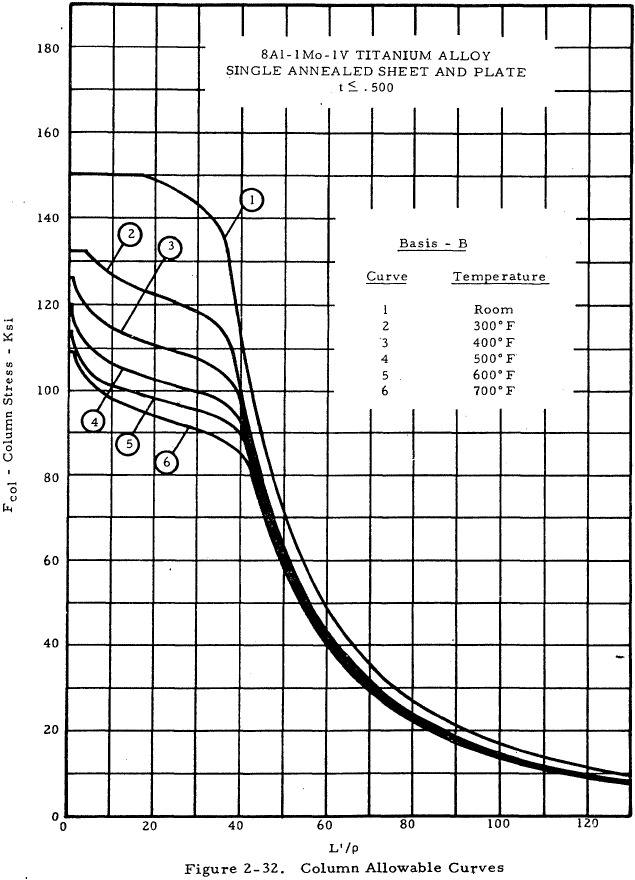
| 8Al-1Mo-1V Single Annealed Sheet and Plate | 2-32 |
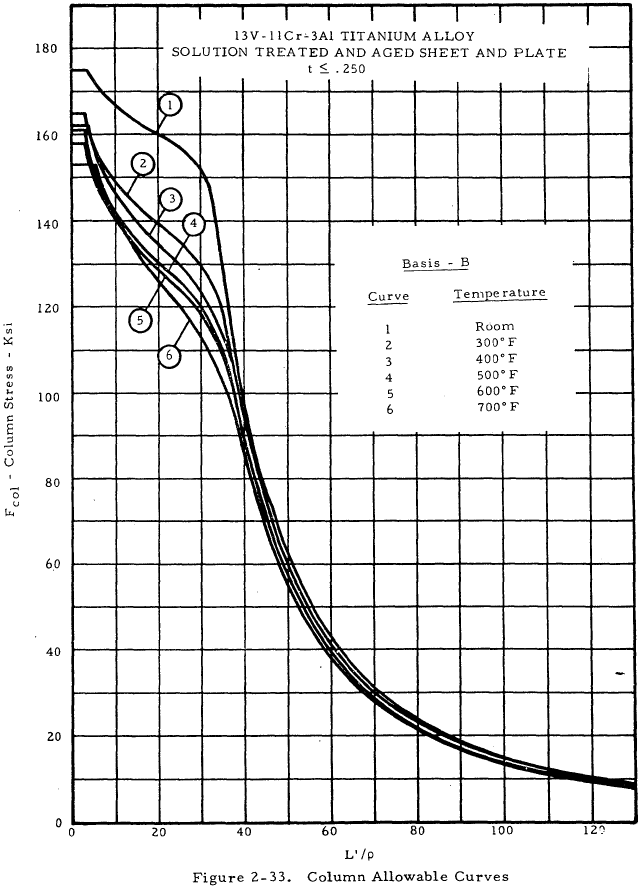
| 13V-11Cr-3Al Solution Treated and Aged Sheet and Plate | 2-33 |
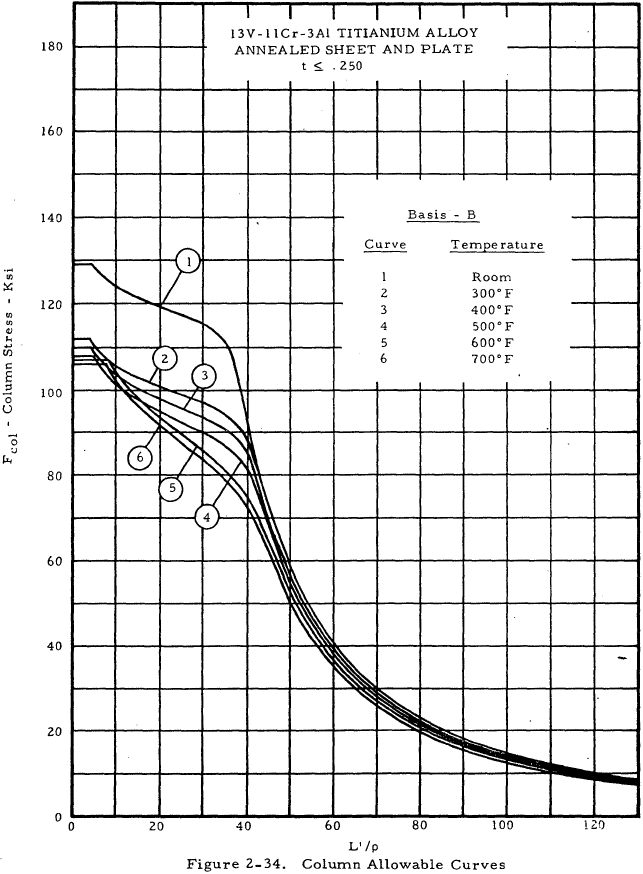
| 13V-11Cr-3Al Annealed Sheet and Plate | 2-34 |
Need a Column Buckling Calculator?
Try this column buckling calculator.
- buckling analysis of long and intermediate-length columns loaded in compression
- loading can be either central or eccentric




Need a Column Buckling Calculator?
Try this column buckling calculator.
- buckling analysis of long and intermediate-length columns loaded in compression
- loading can be either central or eccentric
2.3.1.2 Sample Problem - Column Data Applicable to Both Long and Short Columns
Given: The 0.6 in. square concentrically loaded column shown in Figure 2-35.
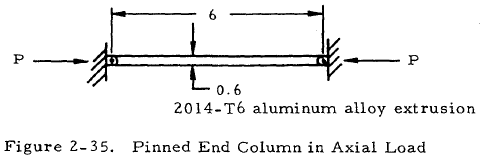
Find: The critical load, Pcr, by using column curves applicable to both long and short columns.
Solution: Since the column is pinned at both ends; L' = L = 6 in. For a square, I = b4/12 and A = b2. Thus,
$$ \rho = \sqrt{ ~I \over A } = \sqrt{ b^2 \over 12 } = \sqrt{ (0.6)^2 \over 12 } = 0.173 ~\text{in} $$ $$ { L' \over \rho } = { 6 ~\text{in} \over 0.173 ~\text{in} } = 34.6 $$From Figure 2-3, curve 2, find Fcol = 56,200 psi. Thus,
$$ P_{cr} = F_{col} A = 56,200 (0.6)^2 = 20,200 ~\text{lb} $$