Shear Web Beam Bending
This page provides the sections on shear web beam bending from the "Stress Analysis Manual," Air Force Flight Dynamics Laboratory, October 1986.
Other related chapters from the Air Force "Stress Analysis Manual" can be seen to the right.
- Simple Beam Bending
- Shear Web Beam Bending
- Partial Tension Beam Bending
- Beam Forces & Moments
- Beam Columns
- Beam Torsion
Nomenclature
| Af | = | cross-sectional area of tension or compression flange |
| Cr | = | rivet factor |
| E | = | modulus of elasticity |
| Fs | = | allowable web shear stress |
| Fscoll | = | collapsing shear stress for solid unstiffened webs |
| Fscr | = | critical (or initial) buckling stress |
| fb | = | calculated primary bending stress |
| fs | = | calculated shear stress |
| h | = | height of shear web beam between centroids of flanges |
| I | = | moment of inertia |
| Iu | = | moment of inertia of upright or stiffener about its base |
| M | = | applied bending moment |
| p | = | rivet spacing |
| q | = | shear flow |
| t | = | thickness |
| V | = | shear force |
| η | = | plasticity coefficient |
1.3.2 Introduction to Shear Web Beams in Bending
The most efficient type of beam is one in which the material resisting bending is concentrated as near the extreme fiber as possible and the material resisting shear is a thin web connecting tension and compression flanges. The simplifying assumption that all the mass is concentrated at the centroids of the flanges may be made for such beams, thus reducing the simple beam formulas to fb = M/Af h for bending and to fs = V/ht for shear. The flanges resist all bending and the web resists all shear.
These beams are divided into two types, shear resistant and partial tension field beams. The webs of shear resistant beams resist the shear load without buckling, and the webs of partial tension field beams buckle at less than the maximum beam load.
If \( \sqrt{V}/h \) is less than seven, the use of a partial tension beam is recommended on the basis of weight economy; and the use of a shear resistant beam is recommended if \( \sqrt{V}/h \) is greater than eleven. If \( 7 < \sqrt{V}/h < 11 \), factors other than weight will determine the type of beam used.
1.3.2.1 Introduction to Shear Resistant Beams in Bending
If the web of a shear resistant beam is sufficiently thin, the simplifying assumption that all the mass is concentrated at the centroids of the flanges may be made. This reduces the simple beam formulas to
for bending, and
for shear. The flanges resist all of the bending and the webs resist all of the shear. Unstiffened shear resistant beams are discussed in Section 1.3.2.2 while stiffened shear resistant beams are treated in Section 1.3.2.3.
Need a Beam Calculator?
Try this beam calculator.
- Calculates stresses and deflections in straight beams
- Builds shear and moment diagrams
- Can specify any configuration of constraints, concentrated forces, and distributed forces
1.3.2.2 Unstiffened Shear Resistant Beams in Bending
Both the web and flanges of an unstiffened shear resistant beam must be checked for failure. The flange is generally considered to have failed if the bending stress in it exceeds the yield stress of the material, although bending in the plastic range may be used if some permanent set can be permitted.
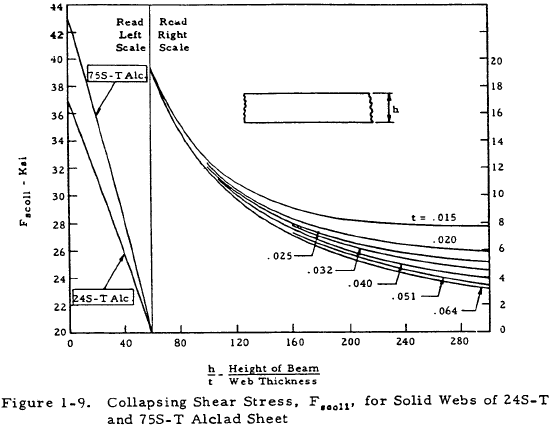
The web must be checked for ultimate load as well as for collapse. If the web is not subject to collapse, the allowable average stress at ultimate load, \(F_s\) will be either 85% of the ultimate strength in shear or 125% of the yield strength in shear. Figure 1-9 gives the collapsing stress for two aluminum alloys. It should be noted that for thinner webs (h/t > 60), initial buckling does not cause collapse.
In conclusion, the required thickness of a thin unstiffened web is given by
or
whichever is larger.
1.3.2.3 Stiffened Shear Resistant Beams in Bending
The vertical stiffeners in a shear resistant beam resist no compressive load, as is the case for tension field beams, but only divide the web into smaller unsupported rectangles, thus increasing the web buckling stress. The flange web and rivets of such a beam must be analyzed.
1.3.2.4 Flanges of Stiffened Shear Resistant Beams
The flanges of a stiffened shear-resistant beam must be checked for yielding or ultimate strength by means of Equation (1-15) as in the case of unstiffened shear resistant beams.
1.3.2.5 Webs of Stiffened Shear Resistant Beams
The web panel of a stiffened shear-resistant beam must be checked for strength as well as for stability.
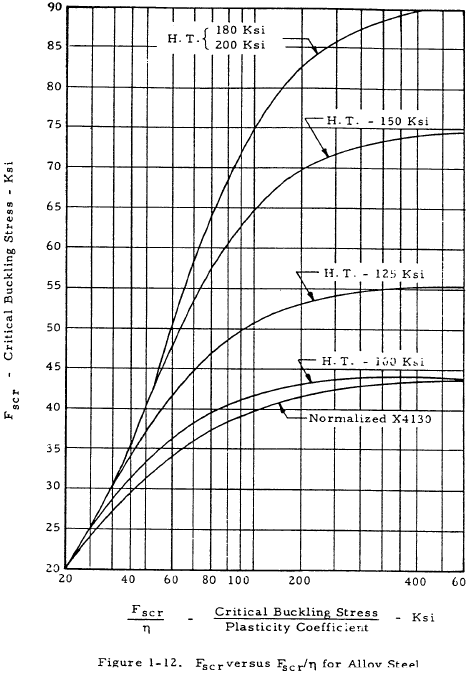
The strength of such a web may be checked by Equation (1-16) as in the case of unstiffened shear resistant beams, and the stability of such a beam may be checked by Equation (1-19) in conjunction with Figures 1-10 through 1-16.

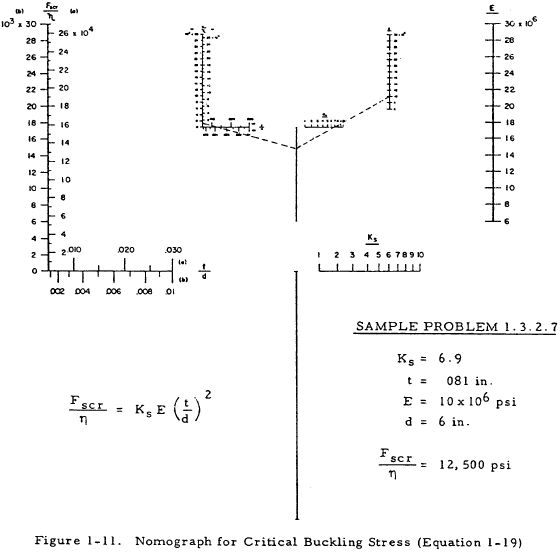
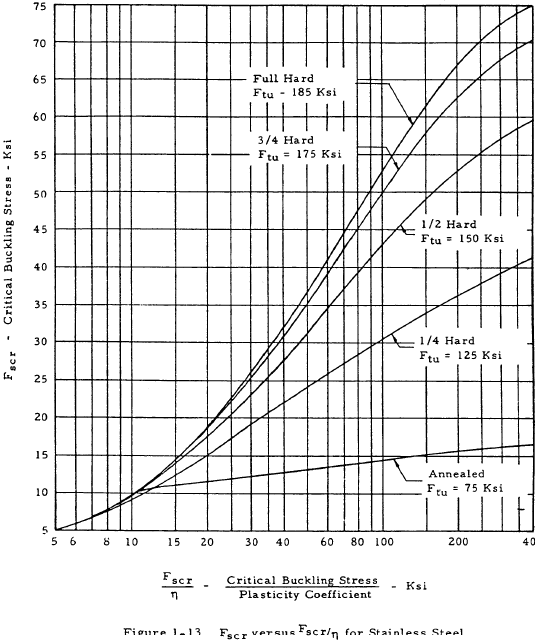

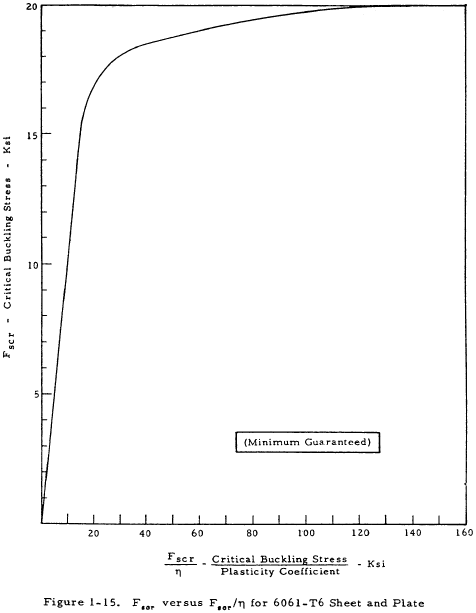
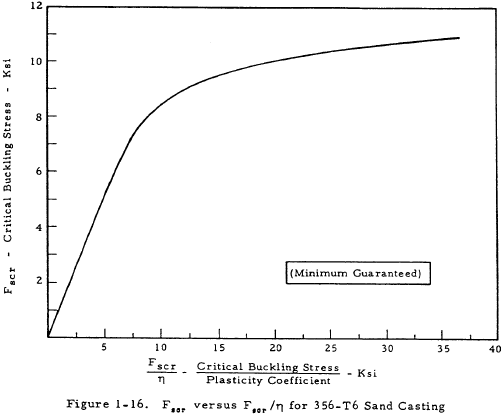
The critical buckling stress of a web panel of height h, width d, and thickness t, is given by
In this equation, Ks is a function of d/h and the edge restraint of the web panel. Figure 1-10 relates Ks to d/h and Iu/ht3. Once Ks has been found, Fscr/η may be obtained from the nomogram in Figure 1-11. Fscr may then be found from Figures 1-12 through 1-16. It should be noted that the moment of inertia of the stiffener, Iu, for Figure 1-10 should be calculated about the base of the stiffener (where the stiffener connects to the web). Also, the modulus of elasticity of the web has been assumed to be equal to that of the stiffeners.
Need a Beam Calculator?
Try this beam calculator.
- Calculates stresses and deflections in straight beams
- Builds shear and moment diagrams
- Can specify any configuration of constraints, concentrated forces, and distributed forces
1.3.2.6 Rivets in Shear Resistant Beams
Rivets are required to fasten the web to flange in shear resistant beams. In addition, rivets are used to fasten the web to the stiffener and the stiffeners to the flange in stiffened shear resistant beams.
1.3.2.6.1 Web-to-Flange Rivets in Shear Resistant Beams
The spacing and size of web-to-flange rivets should be such that the rivet allowable (bearing or shear) divided by q×p (the applied web shear flow times the rivet spacing) gives the proper margin of safety. The rivet factor, Cr (rivet spacing - rivet diameter/rivet spacing), should not be less than 0.6 for good design and in order to avoid undue stress concentration.
1.3.2.6.2 Web-to-Stiffener Rivets in Shear Resistant Beams
No exact information is available on the strength required of the attachment of stiffeners to web in shear resistant beams. The data in Table 1-4 is recommended.
| Web Thickness, in. | Rivet Size | Rivet Spacing, in. |
|---|---|---|
| 0.025 | AD 3 | 1.00 |
| 0.032 | AD 4 | 1.25 |
| 0.040 | AD 4 | 1.10 |
| 0.051 | AD 4 | 1.00 |
| 0.064 | AD 4 | 0.90 |
| 0.072 | AD 5 | 1.10 |
| 0.081 | AD 5 | 1.00 |
| 0.091 | AD 5 | 0.90 |
| 0.102 | DD 6 | 1.10 |
| 0.125 | DD 6 | 1.00 |
| 0.156 | DD 6 | 0.90 |
| 0.188 | DD 8 | 1.00 |
1.3.2.6.3 Stiffener-to-Flange Rivets in Shear Resistant Beams
No information is available on the strength required of the attachment of the stiffeners to flange. It is recommended that one rivet the next size larger than that used in the attachment of stiffeners to web or two rivets the same size be used whenever possible.
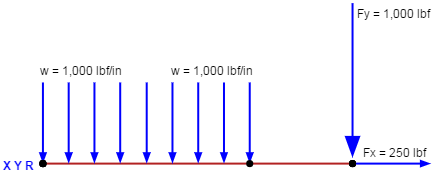
1.3.2.7 Sample Problem - Stiffened Shear Resistant Beams
Given: The beam shown in Figure 1-17 made of 75S-T6 Alclad.
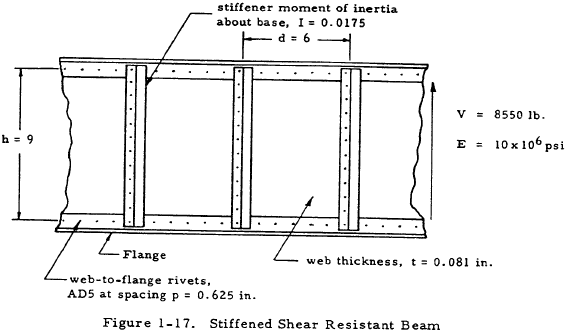
Find: The margin of safety of the web and the load on each web to flange rivet.
Solution: From Equation (1-16) the web shear stress is given by
$$ F_s = { V \over h ~t } = { 8550 \over 9 (0.081) } = 11,720 ~\text{psi} $$ $$ { d \over h } = { 6 \over 9 } = 0.667 $$and
$$ { I_u \over h ~t^3 } = { 0.0175 \over 9 (0.081)^3 } = 3.66 $$From Figure 1-10, Ks = 6.9. From Figure 1-11, Fscr/η = 12,500 psi. From Figure 1-14, Fscr = 12,500 psi.
Since the critical buckling stress of the web is less than the yield stress, the most likely type of failure is buckling. Thus, the margin of safety of the web may be given by
$$ M.S. = { F_{scr} \over f_s } - 1 = { 12500 \over 11720 } - 1 = 0.06 $$The load per web-to-flange rivet is
$$ q \times p = { V \over h } ~p = { 8550 \over 9 } (0.625) = 594 ~\text{lb} $$