Membranes

This page provides the chapter on the analysis of membranes from the "Stress Analysis Manual," Air Force Flight Dynamics Laboratory, October 1986.

7.1 Introduction to Membranes

A membrane may be defined to be a plate that is so thin that it may be considered to have no bending rigidity. The only stresses present are in the plane of the surface and are uniform throughout the thickness of the membrane.

Section 7.3 of this chapter treats of circular membranes, and Section 7.5 deals with square and rectangular membranes.

7.2 Nomenclature for Membranes

a	=	longitudinal dimension of membrane
D	=	diameter
E	=	modulus of elasticity
f	=	calculated stress
f_max	=	calculated maximum stress
n₁-n₇	=	coefficients given in Figure 7-9
p	=	pressure

R	=	outside radius of circular membrane
r	=	cylindrical coordinate
t	=	thickness of membrane
x, y	=	rectangular coordinates
δ	=	deflection
δ_c	=	center deflection of circular membrane
μ	=	Poisson's ratio

7.3 Circular Membranes

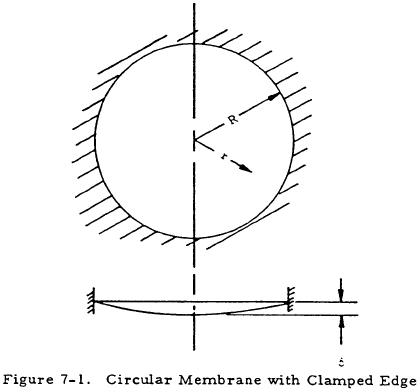
Figure 7-1 shows two views of a circular membrane with the clamped edge under a uniform pressure, p.

The maximum deflection of this membrane is at the center and is given by

$$ \delta_c = 0.662 ~R ~\sqrt[\uproot{1} \scriptstyle 3]{ p ~R \over E ~t } $$

(7-1)

The deflection of the membrane at a distance, r, from the center is

$$ \delta = \delta_c \left[ 1 - 0.09 \left({ r \over R }\right)^2 - 0.1 \left({ r \over R }\right)^5 \right] $$

(7-2)

The stress at the center of this membrane is

$$ f = 0.423 ~\sqrt[\uproot{1} \scriptstyle 3]{ E ~p^2 R^2 \over t^2 } $$

(7-3)

while that at the edge is

$$ f = 0.328 ~\sqrt[\uproot{1} \scriptstyle 3]{ E ~p^2 R^2 \over t^2 } $$

(7-4)

7.4 Sample Problem - Circular Membranes

Given: The circular membrane shown in Figure 7-2

Find: The center deflection and the stresses at the center and at the edge of the membrane.

Solution:

$$ {p \over E} \left({ D \over t }\right)^4 = { 10 \over 10 \times 10^6 } \left({ 15 \over 0.1 }\right)^4 = 506 $$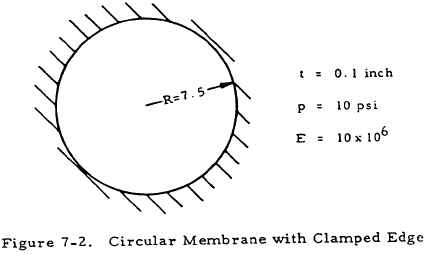

From Section 7.5.3.2, a square plate, for which p/E (b/t)⁴ is greater than 250, may be considered to be a membrane. Assuming this to be approximately true for a circular plate with D used in the relation instead of b, the given plate may be treated as a membrane.

From Equation (7-1), the center deflection of the given membrane is

$$ \delta_c = 0.662 ~R ~\sqrt[\uproot{1} \scriptstyle 3]{ p ~R \over E ~t } = 0.662 (7.5) ~\sqrt[\uproot{1} \scriptstyle 3]{ 10 (7.5) \over 10^7 (0.1) } = 0.21 ~\text{in} $$

From Equation (7-3), the stress at the center of the membrane is

$$ f = 0.423 ~\sqrt[\uproot{1} \scriptstyle 3]{ E ~p^2 R^2 \over t^2 } = 0.423 ~\sqrt[\uproot{1} \scriptstyle 3]{ 10^7 (10^2) (7.5^2) \over (0.1)^2 } = 7,500 ~\text{psi} $$

From Equation (7-4), the stress at the edge of the membrane is

$$ f = 0.328 ~\sqrt[\uproot{1} \scriptstyle 3]{ E ~p^2 R^2 \over t^2 } = 0.328 ~\sqrt[\uproot{1} \scriptstyle 3]{ 10^7 (10^2) (7.5^2) \over (0.1)^2 } = 5,870 ~\text{psi} $$

Need Structural Calculators?

We have a number of structural calculators to choose from. Here are just a few:

7.5 Rectangular Membranes

For purposes of analysis, rectangular membranes may be divided into two classes: long rectangular membranes where the ratio of length to width (a/b) is greater than five, and short rectangular membranes where this ratio is less than five.

7.5.1 Long Rectangular Membranes

Figure 7-3 shows a long rectangular membrane (a/b > 5) clamped along all four sides.

Long Rectangular Membrane Clamped on Four Sides

The deflection and stress at the center of such a plate are approximately the same as those in a long membrane clamped along the two long sides. Such a membrane is shown in its deflected position in Figure 7-4.

Long Rectangular Membrane Clamped on Two Sides

The maximum stress and center deflection of the membrane in Figure 7-4 under uniform pressure pare given by Equations (7-5) and (7-6).

$$ f_{max} = \left[{ p^2 E ~b^2 \over 24 ~(1 - \mu^2) ~t^2 }\right]^{1/3} $$

(7-5)

$$ {\delta \over b} = {1 \over 8} \left[{ 24 ~(1 - \mu^2) ~p ~b \over E ~t }\right]^{1/3} $$

(7-6)

These equations are presented graphically in Figures 7-5 and 7-6 for μ = 0.3.

Maximum Stress in Long Rectangular Membranes Held Along Long Sides

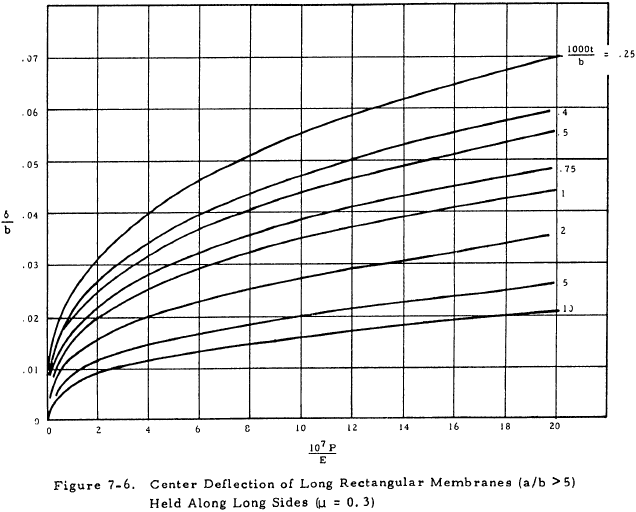
Center Deflection of Long Rectangular Membranes Held Along Long Sides

A long rectangular plate may be considered to be a membrane if p/E (b/t)⁴ is greater than 100.

7.5.2 Sample Problem - Long Rectangular Membrane

Given: The membrane shown in Figure 7-7.

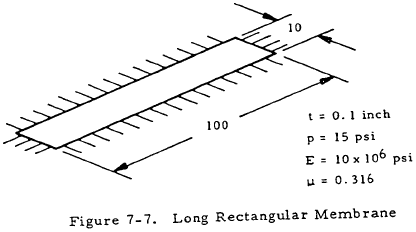
Find: The maximum stress and center deflection

Solution:

$$ {p \over E} \left({b \over t}\right)^4 = {15 \over 10 \times 10^6} \left({10 \over 0.1}\right)^4 = 150 $$

Since this quantity is greater than 100, the given plate may indeed be considered to be a membrane.

From Equation (7-5),

$$ f_{max} = \left[{ p^2 E ~b^2 \over 24 ~(1 - \mu^2) ~t^2 }\right]^{1/3} = \left[{ 15^2 (10^7) ~(10^2) \over 24 ~(1 - 0.316^2) (0.1^2) }\right]^{1/3} = 10130 $$

From Equation (7-6),

$$ {\delta \over b} = {1 \over 8} \left[{ 24 ~(1 - \mu^2) ~p ~b \over E ~t }\right]^{1/3} = {1 \over 8} \left[{ 24 ~(1 - 0.316^2) (15)(10) \over 10^7 (0.1) }\right]^{1/3} = 0.0185 $$

Thus,

$$ \delta = 0.0185 ~b = 0.0185 (10) = 0.185 ~\text{in} $$

For quick calculations, the graphs in Figures 7-5 and 7-6 could have been used. However, this procedure would give answers that are not theoretically exact since these graphs are based on a Poisson's ratio of 0.3 rather than 0.316.

Need Structural Calculators?

We have a number of structural calculators to choose from. Here are just a few:

7.5.3 Short Rectangular Membranes

7.5.3.1 Theoretical Results for Short Rectangular Membranes

Figure 7-8 shows a short rectangular membrane (a/b < 5) clamped on four sides under a uniform pressure p.

Short Rectangular Membrane Clamped on Four sides

The deflection at the center of such a membrane is

$$ \delta = n_1 a ~\sqrt[\uproot{1} \scriptstyle 3]{ p ~a \over E ~t } $$

(7-7)

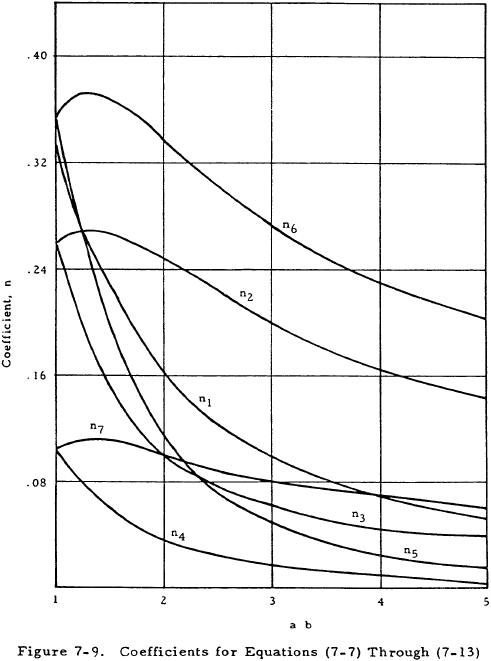
where n₁ is given in Figure 7-9.

The stresses at various locations on short rectangular membranes are given by the following equations for which the values of the coefficients n₂ through n₇ are given in Figure 7-9.

Coefficients for Equations (7-7) Through (7-13)

Center of plate (x = b/2, y = a/2)

$$ f_x = n_2 ~\sqrt[\uproot{1} \scriptstyle 3]{ p^2 E ~\left({ a \over t }\right)^2 } $$

(7-8)

$$ f_y = n_3 ~\sqrt[\uproot{1} \scriptstyle 3]{ p^2 E ~\left({ a \over t }\right)^2 } $$

(7-9)

Center of short side (x = b/2, y = 0)

$$ f_x = n_4 ~\sqrt[\uproot{1} \scriptstyle 3]{ p^2 E ~\left({ a \over t }\right)^2 } $$

(7-10)

$$ f_y = n_5 ~\sqrt[\uproot{1} \scriptstyle 3]{ p^2 E ~\left({ a \over t }\right)^2 } $$

(7-11)

Center of long side (x = 0, y = a/2)

$$ f_x = n_6 ~\sqrt[\uproot{1} \scriptstyle 3]{ p^2 E ~\left({ a \over t }\right)^2 } $$

(7-12)

$$ f_y = n_7 ~\sqrt[\uproot{1} \scriptstyle 3]{ p^2 E ~\left({ a \over t }\right)^2 } $$

(7-13)

It should be noted that the maximum membranes stress occurs at the center of the long side of the plate.

7.5.3.2 Applicability of Theoretical Results for Short Rectangular Membranes

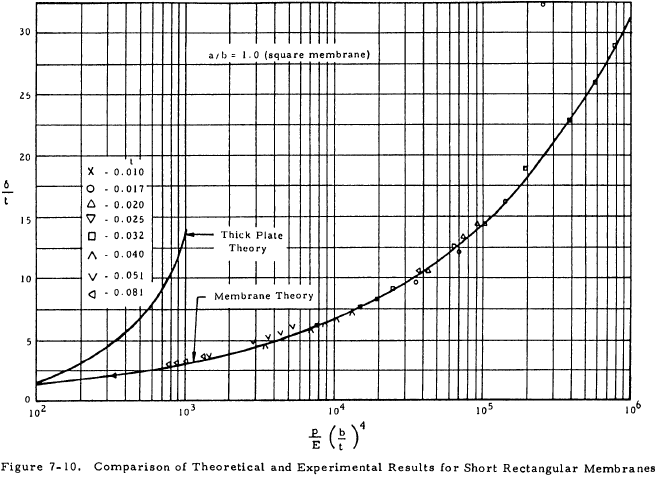
Figures 7-10 and 7-11 give the deflections of plates with various length-to-width ratios obtained from the equations in Section 7.5.3.1 and compare these deflections with experimental values for 10-inch-wide aluminum plates.

For square plates (a/b = 1.0), the thick plate theory should be used for values of (p/E) (b/t)⁴ from 0 to 100. If 100 < (p/E) (b/t)⁴ < 250, no theoretical method compares closely with test although the membrane theory should be used for conservative results. If (p/E) (b/t)⁴ is greater than 250, the membrane theory produces results that compare closely with experiments for square plates.

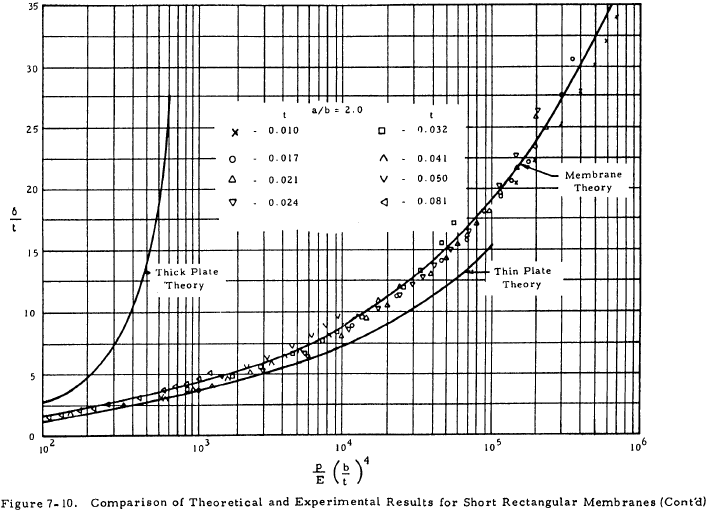
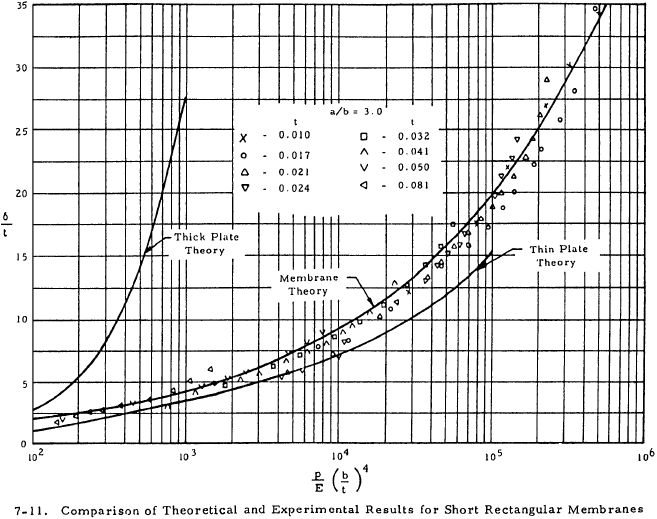
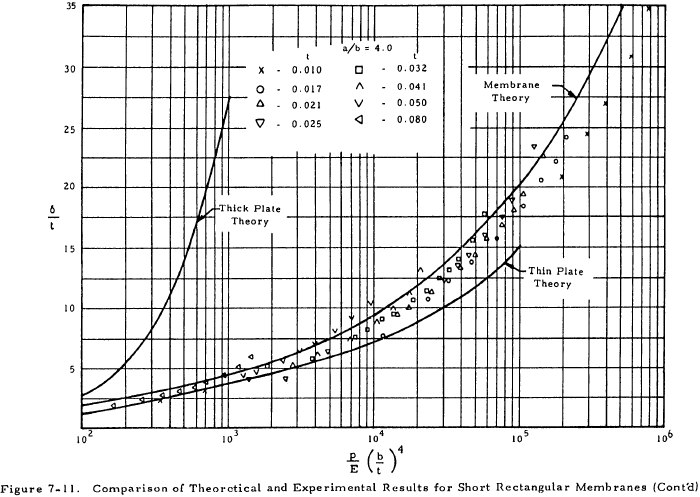
Comparison of Theoretical and Experimental Results for Short Rectangular Membranes

A rectangular plate (a/b > 1.0) may be considered as a membrane if (p/E) (b/t)⁴ > 100, with results becoming more conservative as a/b decreases.

7.5.3.3 Sample Problem - Short Rectangular Membranes

Given: The membrane shown in Figure 7-12

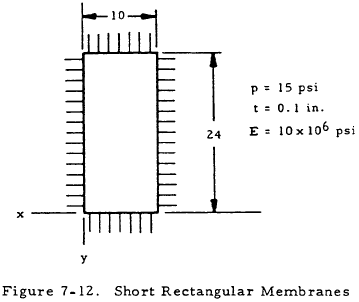
Find: The center deflection and stresses

Solution:

$$ \left({p \over E}\right) \left({b \over t}\right)^4 = {15 \over 10^7} \left({10 \over 0.1}\right)^4 = 150 $$

Since this value is greater than 100, the given plate may be treated by membrane equations, according to Section 7.5.3.2.

$$ {a \over b} = {24 \over 10} = 2.4 $$

From Figure 7-9:

n₁ = 0.130	n₅ = 0.077
n₂ = 0.230	n₆ = 0.311
n₃ = 0.080	n₇ = 0.090
n₄ = 0.026

From Equation (7-7), the deflection of the center of the membrane is

$$ \delta = n_1 a ~\sqrt[\uproot{1} \scriptstyle 3]{ p ~a \over E ~t } = 0.130 (24) ~\sqrt[\uproot{1} \scriptstyle 3]{ 15 (24) \over 10^7 (0.1) } = 0.222 ~\text{in} $$

From Equation (7-8) through (7-13), the stresses in the membrane are as follows:

Center of plate (x = 5, y = 12)

$$ f_x = n_2 ~\sqrt[\uproot{1} \scriptstyle 3]{ p^2 E ~\left({ a \over t }\right)^2 } = 0.230 ~\sqrt[\uproot{1} \scriptstyle 3]{ (15)^2 (10^7) ~\left({ 24 \over 0.1 }\right)^2 } = 11,650 ~\text{psi} $$

$$ f_y = n_3 ~\sqrt[\uproot{1} \scriptstyle 3]{ p^2 E ~\left({ a \over t }\right)^2 } = 0.080 ~\sqrt[\uproot{1} \scriptstyle 3]{ (15)^2 (10^7) ~\left({ 24 \over 0.1 }\right)^2 } = 4,050 ~\text{psi} $$

Center of short side (x = 5, y = 0)

$$ f_x = n_4 ~\sqrt[\uproot{1} \scriptstyle 3]{ p^2 E ~\left({ a \over t }\right)^2 } = 0.026 ~\sqrt[\uproot{1} \scriptstyle 3]{ (15)^2 (10^7) ~\left({ 24 \over 0.1 }\right)^2 } = 1,315 ~\text{psi} $$

$$ f_y = n_5 ~\sqrt[\uproot{1} \scriptstyle 3]{ p^2 E ~\left({ a \over t }\right)^2 } = 0.077 ~\sqrt[\uproot{1} \scriptstyle 3]{ (15)^2 (10^7) ~\left({ 24 \over 0.1 }\right)^2 } = 3,900 ~\text{psi} $$

Center of long side (x = 0, y = 12)

$$ f_x = n_6 ~\sqrt[\uproot{1} \scriptstyle 3]{ p^2 E ~\left({ a \over t }\right)^2 } = 0.311 ~\sqrt[\uproot{1} \scriptstyle 3]{ (15)^2 (10^7) ~\left({ 24 \over 0.1 }\right)^2 } = 15,750 ~\text{psi} $$

$$ f_y = n_7 ~\sqrt[\uproot{1} \scriptstyle 3]{ p^2 E ~\left({ a \over t }\right)^2 } = 0.090 ~\sqrt[\uproot{1} \scriptstyle 3]{ (15)^2 (10^7) ~\left({ 24 \over 0.1 }\right)^2 } = 4,550 ~\text{psi} $$

The greatest stress is 15,750 psi at the center of the long side.