Heat Generation
This page provides the chapter on heat generation from the "DOE Fundamentals Handbook: Thermodynamics, Heat Transfer, and Fluid Flow," DOE-HDBK-1012/2-92, U.S. Department of Energy, June 1992.
Other related chapters from the "DOE Fundamentals Handbook: Thermodynamics, Heat Transfer, and Fluid Flow" can be seen to the right.
Heat Generation
Heat generation and power output in a reactor are related. Reactor power is related to the mass flow rate of the coolant and the temperature difference across the reactor core.
Heat Generation
The heat generation rate in a nuclear core is directly proportional to the fission rate of the fuel and the thermal neutron flux present. On a straight thermodynamic basis, this same heat generation is also related to the fluid temperature difference across the core and the mass flow rate of the fluid passing through the core. Thus, the size of the reactor core is dependent upon and limited by how much liquid can be passed through the core to remove the generated thermal energy. Many other factors affect the amount of heat generated within a reactor core, but its limiting generation rate is based upon how much energy can safely be carried away by the coolant.
The fission rate within a nuclear reactor is controlled by several factors. The density of the fuel, the neutron flux, and the type of fuel all affect the fission rate and, therefore, the heat generation rate. The following equation is presented here to show how the heat generation rate (\( \dot{Q} \)) is related to these factors. The terms will be discussed in more detail in the Nuclear Science modules.
where:
| \( \dot{Q} \) | = | heat generation rate (Btu/sec) |
| G | = | energy produced per fission (Btu/fission) |
| N | = | number of fissionable fuel nuclei/unit volume (atoms/cm3) |
| σf | = | microscopic fission cross-section of the fuel (cm2) |
| ϕ | = | neutron flux (n/cm2-sec) |
| Vf | = | volume of the fuel (cm3) |
The thermal power produced by a reactor is directly related to the mass flow rate of the reactor coolant and the temperature difference across the core. The relationship between power, mass flow rate, and temperature is given in Equation 2-15.
where:
| \( \dot{Q} \) | = | heat generation rate (Btu/hr) |
| \( \dot{m} \) | = | mass flow rate (lbm/hr) |
| cp | = | specific heat capacity of reactor coolant system (Btu/lbm-°F) |
| ΔT | = | temperature difference across core (°F) |
For most types of reactors (boiling water reactor excluded), the temperature of the coolant is dependent upon reactor power and coolant flow rate. If flow rate is constant, temperature will vary directly with power. If power is constant, temperature will vary inversely with flow rate.
Flux Profiles
Once the type and amount of fuel is determined, the shape of the neutron flux distribution along the core is established. Both radial and axial flux distributions must be determined. A radial distribution looks at flux from the center of the core out to the edges. An axial distribution looks at flux from the bottom to the top of the core. As seen in Equation 2-14, the fission rate directly affects the heat generation rate within a reactor core. In the core regions of highest flux, the highest heat generation rate will be present.
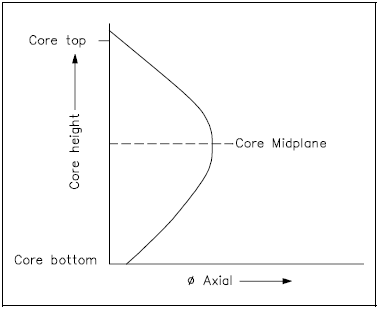
Many factors affect the axial and radial flux distributions, including the number and type of control rods, the geometry and size of core, the concentration of fission product poisons, and reflector properties. The peak power production regions within each distribution normally occurs near the center of the core, as indicated in Figures 14 and 15, but can vary during transients or as the core ages.
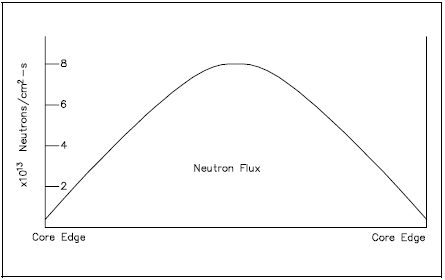
The above figures represent the neutron flux profiles without considering the effects of control rods. Once control rods and reflectors are taken into account, the flux profiles become much flatter although the peak still occurs near the center.
The shape of the profiles can be determined by measuring the ratio of the peak flux to the average flux in the distribution. This peaking factor is referred to as the hot channel factor. A hot channel factor of 1.0 would imply a flat flux profile.
Thermal Limits
Hot channel factors are calculated values used to take into account various uncertainties in tolerances used in core manufacturing. For example, consider a coolant channel of the minimum acceptable width and length, that happens to be adjacent to a fuel plate with the maximum acceptable fuel loading. In this channel, we would now have less water than in the average channel, receiving more heat than the normal coolant channel. For any given values of core power and flow, this hypothetical channel would be closest to a thermal limit. Therefore, all design considerations are based upon the hot channel factor for each core. The nuclear heat flux hot channel factor (HFHCF) is the ratio of the maximum heat flux expected at any area to the average heat flux for the core. The nuclear enthalpy rise hot channel factor is the ratio of the total kW heat generation along the fuel rod with the highest total kW to the total kW of the average fuel rod.
Thus the limitation of the peak flux value in a core is directly related to the hot channel factor. However, in discussing flux profiles, "average" values of flux in the core are usually referred to rather than peaks.
Average Linear Power Density
In nuclear reactors, the fuel is usually distributed in individual components which sometimes resemble rods, tubes, or plates. It is possible to determine the average power produced per unit length of fuel component by dividing the total thermal output of the core by the total length of all the fuel components in the core. This quantity is called the average linear power density. Common units for measuring average linear power density are kW/ft.
Example:
Calculate the average linear power density for an entire core if a 3400 MW reactor is operating at full power.
| Core data is: | each fuel rod is 12 ft long |
| 264 rods/fuel assembly | |
| 193 fuel assemblies in the core |
Solution:
Maximum Local Linear Power Density
The maximum local linear power density when compared to the average linear power density results in the definition of the nuclear heat flux hot channel factor. The nuclear heat flux hot channel factor can be looked at as having axial and radial components that are dependent upon the power densities and, thus, the flux in the radial and axial planes of the core. Once the hot channel factor is known, the maximum local linear power density anywhere in the core can be determined, as demonstrated in the following example.
Example:
If the nuclear heat flux hot channel factor is 1.83, calculate the maximum local linear power density in the core for the previous example (the average linear power density problem).
Solution:
| Maximum linear power density | = | HFHCF (Av linear power density) |
| = | 1.83 (5.56) kW/ft | |
| = | 10.18 kW/ft |
Normally, nuclear facility operators are provided with the above core power and heat generation distributions, rather than having to calculate them. In addition, various monitoring systems are always employed to provide the operator with a means of monitoring core performance and the proximity of the existing operating conditions to core operational limitations.
Temperature Profiles
Additional areas of interest are the temperature profiles found within the core. A typical axial temperature profile along a coolant channel for a pressurized water reactor (PWR) is shown in Figure 16. As would be expected, the temperature of the coolant will increase throughout the entire length of the channel.
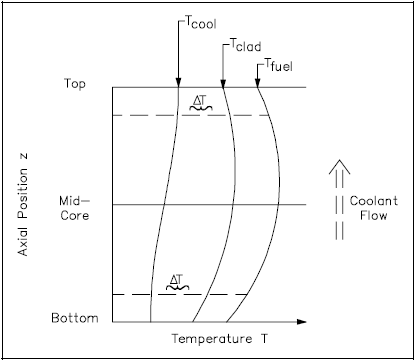
However, the rate of increase will vary along with the linear heat flux of the channel. The power density and linear heat rate will follow the neutron flux shape. However, the temperature distributions are skewed by the changing capacity of the coolant to remove the heat energy. Since the coolant increases in temperature as it flows up the channel, the fuel cladding and, thus, the fuel temperatures are higher in the upper axial region of the core.
A radial temperature profile across a reactor core (assuming all channel coolant flows are equal) will basically follow the radial power distribution. The areas with the highest heat generation rate (power) will produce the most heat and have the highest temperatures. A radial temperature profile for an individual fuel rod and coolant channel is shown in Figure 17. The basic shape of the profile will be dependent upon the heat transfer coefficient of the various materials involved. The temperature differential across each material will have to be sufficient to transfer the heat produced. Therefore, if we know the heat transfer coefficient for each material and the heat flux, we can calculate peak fuel temperatures for a given coolant temperature.
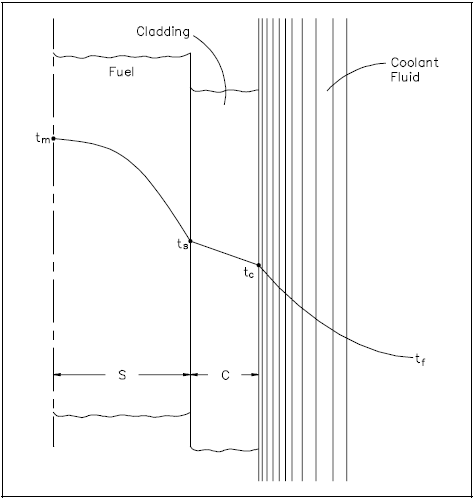
Volumetric Thermal Source Strength
The total heat output of a reactor core is called the heat generation rate. The heat generation rate divided by the volume of fuel will give the average volumetric thermal source strength. The volumetric thermal source strength may be used to calculate the heat output of any section of fuel rod, provided the volume of the section is known.
Fuel Changes During Reactor Operation
During the operation of a nuclear reactor, physical changes occur to the fuel that affect its ability to transfer heat to the coolant. The exact changes that occur are dependant on the type and form of fuel. Some reactors use fuel assemblies that consist of zircalloy tubes containing cylindrical ceramic pellets of uranium dioxide. During manufacture, a small space or gap is left between the fuel pellets and the zircalloy tube (clad). This gap is filled with pressurized helium. As the reactor is operated at power, several physical changes occur in the fuel that affect the gap between the pellets and clad. One change occurs due to high pressure in the coolant outside the clad and the relatively high temperature of the clad during reactor operation. The high temperature and high pressure causes the clad to be pushed in on the pellets by a process referred to as creep. Another physical change is caused by the fission process. Each fission event creates two fission product atoms from a fuel atom. Even though each fission product atom is roughly half the mass of the fuel atom, the fission products take up more volume than the original fuel atom. Fission products that are gases can collect together and form small gas bubbles within the fuel pellet. These factors cause the fuel pellets to swell, expanding them out against the clad. So the two processes of pellet swell and clad creep both work to reduce the gap between the fuel and clad.
This change in the gap between the pellet and clad has significant impact on heat transfer from the fuel and operating fuel temperatures. Initially a significant temperature difference exists across the gap to cause heat transfer to take place by convection through the helium gas. As the size of the gap is reduced, a smaller temperature difference can maintain the same heat flux. When the fuel pellets and clad come in contact, heat transfer by conduction replaces convection and the temperature difference between the fuel surface and clad decreases even more. Due to the processes of pellet swell and clad creep, the fuel temperatures of some reactors decrease slightly over time while the heat flux from the fuel and therefore the power of the reactor remain constant.
Not all changes that occur to the fuel during reactor operation work to enhance heat transfer. If the chemistry of the coolant is not carefully controlled within appropriate limits, chemical reactions can take place on the surface of the clad, resulting in the formation of a layer of corrosion products or crud between the metal of the clad and the coolant. Typically, this layer will have a lower thermal conductivity than that of the clad material, so it will act as an insulating blanket, reducing heat transfer.
If this corrosion layer is allowed to form, a larger temperature difference will be required between the coolant and fuel to maintain the same heat flux. Therefore, operation at the same power level will cause higher fuel temperatures after the buildup of corrosion products and crud.



