DOE Handbook:
Heat Transfer
  1. Terminology
  2. Conduction
  3. Convection
  4. Radiant Heat Transfer
  5. Heat Exchangers
  6. Boiling Heat Transfer
  7. Heat Generation
  8. Decay Heat
Structural Calculators

Check out these structural calculators:  • Beam Analysis   • Bolted Joints   • Lug Analysis  • Column Buckling

Structural Calculators

Heat Exchangers

This page provides the chapter on heat exchangers from the "DOE Fundamentals Handbook: Thermodynamics, Heat Transfer, and Fluid Flow," DOE-HDBK-1012/2-92, U.S. Department of Energy, June 1992.

Other related chapters from the "DOE Fundamentals Handbook: Thermodynamics, Heat Transfer, and Fluid Flow" can be seen to the right.

DOE Handbook: Heat Transfer
  1. Heat Transfer Terminology
  2. Conduction Heat Transfer
  3. Convection Heat Transfer
  4. Radiant Heat Transfer
  5. Heat Exchangers
  6. Boiling Heat Transfer
  7. Heat Generation
  8. Decay Heat

Heat Exchangers

Heat exchangers are devices that are used to transfer thermal energy from one fluid to another without mixing the two fluids.

Heat Exchangers

The transfer of thermal energy between fluids is one of the most important and frequently used processes in engineering. The transfer of heat is usually accomplished by means of a device known as a heat exchanger. Common applications of heat exchangers in the nuclear field include boilers, fan coolers, cooling water heat exchangers, and condensers.

The basic design of a heat exchanger normally has two fluids of different temperatures separated by some conducting medium. The most common design has one fluid flowing through metal tubes and the other fluid flowing around the tubes. On either side of the tube, heat is transferred by convection. Heat is transferred through the tube wall by conduction.

Heat exchangers may be divided into several categories or classifications. In the most commonly used type of heat exchanger, two fluids of different temperature flow in spaces separated by a tube wall. They transfer heat by convection and by conduction through the wall. This type is referred to as an "ordinary heat exchanger," as compared to the other two types classified as "regenerators" and "cooling towers."

An ordinary heat exchanger is single-phase or two-phase. In a single-phase heat exchanger, both of the fluids (cooled and heated) remain in their initial gaseous or liquid states. In two-phase exchangers, either of the fluids may change its phase during the heat exchange process. The steam generator and main condenser of nuclear facilities are of the two-phase, ordinary heat exchanger classification.

Single-phase heat exchangers are usually of the tube-and-shell type; that is, the exchanger consists of a set of tubes in a container called a shell (Figure 8). At the ends of the heat exchanger, the tube-side fluid is separated from the shell-side fluid by a tube sheet. The design of two-phase exchangers is essentially the same as that of single-phase exchangers.

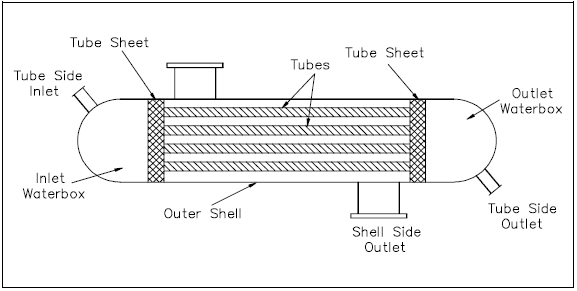
Typical Tube and Shell Heat Exchanger
Figure 8: Typical Tube and Shell Heat Exchanger

Parallel and Counter-Flow Designs

Although ordinary heat exchangers may be extremely different in design and construction and may be of the single- or two-phase type, their modes of operation and effectiveness are largely determined by the direction of the fluid flow within the exchanger.

The most common arrangements for flow paths within a heat exchanger are counter-flow and parallel flow. A counter-flow heat exchanger is one in which the direction of the flow of one of the working fluids is opposite to the direction to the flow of the other fluid. In a parallel flow exchanger, both fluids in the heat exchanger flow in the same direction.

Figure 9 represents the directions of fluid flow in the parallel and counter-flow exchangers. Under comparable conditions, more heat is transferred in a counter-flow arrangement than in a parallel flow heat exchanger.

Fluid Flow Direction
Figure 9: Fluid Flow Direction

The temperature profiles of the two heat exchangers indicate two major disadvantages in the parallel-flow design. First, the large temperature difference at the ends (Figure 10) causes large thermal stresses. The opposing expansion and contraction of the construction materials due to diverse fluid temperatures can lead to eventual material failure. Second, the temperature of the cold fluid exiting the heat exchanger never exceeds the lowest temperature of the hot fluid. This relationship is a distinct disadvantage if the design purpose is to raise the temperature of the cold fluid.

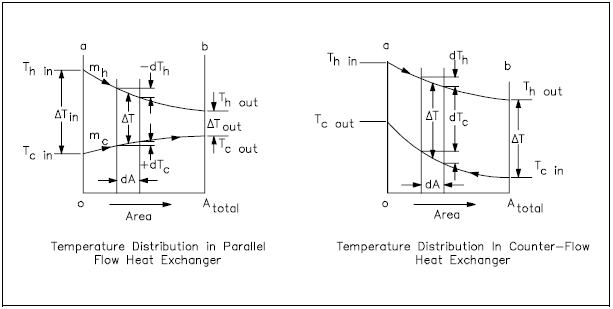
Heat Exchanger Temperature Profiles
Figure 10: Heat Exchanger Temperature Profiles

The design of a parallel flow heat exchanger is advantageous when two fluids are required to be brought to nearly the same temperature.

The counter-flow heat exchanger has three significant advantages over the parallel flow design. First, the more uniform temperature difference between the two fluids minimizes the thermal stresses throughout the exchanger. Second, the outlet temperature of the cold fluid can approach the highest temperature of the hot fluid (the inlet temperature). Third, the more uniform temperature difference produces a more uniform rate of heat transfer throughout the heat exchanger.

Whether parallel or counter-flow, heat transfer within the heat exchanger involves both conduction and convection. One fluid (hot) convectively transfers heat to the tube wall where conduction takes place across the tube to the opposite wall. The heat is then convectively transferred to the second fluid. Because this process takes place over the entire length of the exchanger, the temperature of the fluids as they flow through the exchanger is not generally constant, but varies over the entire length, as indicated in Figure 10. The rate of heat transfer varies along the length of the exchanger tubes because its value depends upon the temperature difference between the hot and the cold fluid at the point being viewed.

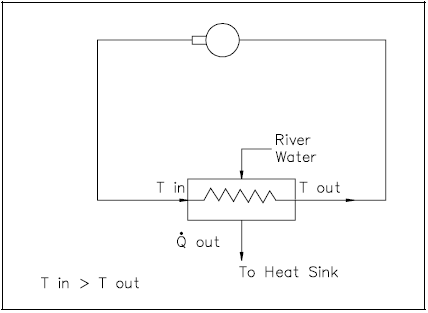
Non-Regenerative Heat Exchanger

Applications of heat exchangers may be classified as either regenerative or non-regenerative. The non-regenerative application is the most frequent and involves two separate fluids. One fluid cools or heats the other with no interconnection between the two fluids. Heat that is removed from the hotter fluid is usually rejected to the environment or some other heat sink (Figure 11).

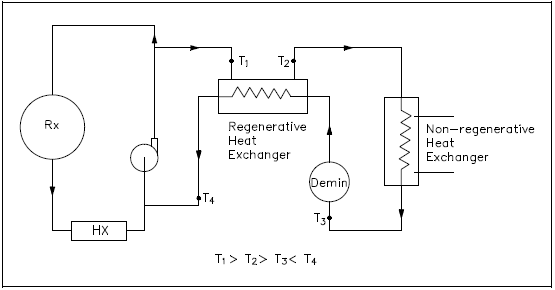
Non-Regenerative Heat Exchanger
Figure 11: Non-Regenerative Heat Exchanger

Regenerative Heat Exchanger

A regenerative heat exchanger typically uses the fluid from a different area of the same system for both the hot and cold fluids. An example of both regenerative and non-regenerative heat exchangers working in conjunction is commonly found in the purification system of a reactor facility. The primary coolant to be purified is drawn out of the primary system, passed through a regenerative heat exchanger, non-regenerative heat exchanger, demineralizer, back through the regenerative heat exchanger, and returned to the primary system (Figure 12).

In the regenerative heat exchanger, the water returning to the primary system is pre-heated by the water entering the purification system. This accomplishes two objectives. The first is to minimize the thermal stress in the primary system piping due to the cold temperature of the purified coolant being returned to the primary system.

The second is to reduce the temperature of the water entering the purification system prior to reaching the non-regenerative heat exchanger, allowing use of a smaller heat exchanger to achieve the desired temperature for purification. The primary advantage of a regenerative heat exchanger application is conservation of system energy (that is, less loss of system energy due to the cooling of the fluid).

Regenerative Heat Exchanger
Figure 12: Regenerative Heat Exchanger

Cooling Towers

The typical function of a cooling tower is to cool the water of a steam power plant by air that is brought into direct contact with the water. The water is mixed with vapor that diffuses from the condensate into the air. The formation of the vapor requires a considerable removal of internal energy from the water; the internal energy becomes "latent heat" of the vapor. Heat and mass exchange are coupled in this process, which is a steady-state process like the heat exchange in the ordinary heat exchanger.

Wooden cooling towers are sometimes employed in nuclear facilities and in factories of various industries. They generally consists of large chambers loosely filled with trays or similar wooden elements of construction. The water to be cooled is pumped to the top of the tower where it is distributed by spray or wooden troughs. It then falls through the tower, splashing down from deck to deck. A part of it evaporates into the air that passes through the tower. The enthalpy needed for the evaporation is taken from the water and transferred to the air, which is heated while the water cools. The air flow is either horizontal due to wind currents (cross flow) or vertically upward in counter-flow to the falling water. The counter-flow is caused by the chimney effect of the warm humid air in the tower or by fans at the bottom (forced draft) or at the top (induced flow) of the tower. Mechanical draft towers are more economical to construct and smaller in size than natural-convection towers of the same cooling capacity.

Log Mean Temperature Difference Application To Heat Exchangers

In order to solve certain heat exchanger problems, a log mean temperature difference (LMTD or ΔTlm) must be evaluated before the heat removal from the heat exchanger is determined. The following example demonstrates such a calculation.

Example:

A liquid-to-liquid counterflow heat exchanger is used as part of an auxiliary system at a nuclear facility. The heat exchanger is used to heat a cold fluid from 120°F to 310°F. Assuming that the hot fluid enters at 500°F and leaves at 400°F, calculate the LMTD for the exchanger.

Solution:

ΔT2 = 400°F − 120°F = 280°F

ΔT1 = 500°F − 310°F = 190°F

$$ \begin{eqnarray} \Delta T_{lm} &=& { (\Delta T_2 - \Delta T_1) \over \ln \left({ \Delta T_2 \over \Delta T_1 }\right) } \nonumber \\ &=& { (280^{\circ}\text{F} - 190^{\circ}\text{F}) \over \ln \left({ 280^{\circ}\text{F} \over 190^{\circ}\text{F} }\right) } \nonumber \\ &=& 232^{\circ}\text{F} \end{eqnarray} $$

The solution to the heat exchanger problem may be simple enough to be represented by a straight-forward overall balance or may be so detailed as to require integral calculus. A steam generator, for example, can be analyzed by an overall energy balance from the feedwater inlet to the steam outlet in which the amount of heat transferred can be expressed simply as \( \dot{Q} = \dot{m} ~\Delta h \), where \( \dot{m} \) is the mass flow rate of the secondary coolant and Δh is the change in enthalpy of the fluid. The same steam generator can also be analyzed by an energy balance on the primary flow stream with the equation \( \dot{Q} = \dot{m} ~c_p ~\Delta T \), where \( \dot{m} \), cp, and ΔT are the mass flow rate, specific heat capacity, and temperature change of the primary coolant. The heat transfer rate of the steam generator can also be determined by comparing the temperatures on the primary and secondary sides with the heat transfer characteristics of the steam generator using the equation \( \dot{Q} = U_o ~A_o ~\Delta T_{lm} \).

Condensers are also examples of components found in nuclear facilities where the concept of LMTD is needed to address certain problems. When the steam enters the condenser, it gives up its latent heat of vaporization to the circulating water and changes phase to a liquid. Because condensation is taking place, it is appropriate to term this the latent heat of condensation. After the steam condenses, the saturated liquid will continue to transfer some heat to the circulating water system as it continues to fall to the bottom (hotwell) of the condenser. This continued cooling is called subcooling and is necessary to prevent cavitation in the condensate pumps.

The solution to condenser problems is approached in the same manner as those for steam generators, as shown in the following example.

Overall Heat Transfer Coefficient

When dealing with heat transfer across heat exchanger tubes, an overall heat transfer coefficient, Uo, must be calculated. Earlier in this module we looked at a method for calculating Uo for both rectangular and cylindrical coordinates. Since the thickness of a condenser tube wall is so small and the cross-sectional area for heat transfer is relatively constant, we can use Equation 2-11 to calculate Uo.

$$ U_o = { 1 \over {1 \over h_1} + { \Delta r \over k } + {1 \over h_2} } $$

Example:

Referring to the convection section of this manual, calculate the heat rate per foot of tube from a condenser under the following conditions. ΔTlm = 232°F. The outer diameter of the copper condenser tube is 0.75 in. with a wall thickness of 0.1 in. Assume the inner convective heat transfer coefficient is 2000 Btu/hr-ft2-°F, and the thermal conductivity of copper is 200 Btu/hr-ft-°F. The outer convective heat transfer coefficient is 1500 Btu/hr-ft2-°F.

Solution:

$$ \begin{eqnarray} U_o &=& { 1 \over {1 \over h_1} + { \Delta r \over k } + {1 \over h_2} } \nonumber \\ &=& { 1 \over {1 \over 2000} + {0.1 ~\text{in} \over 200} { 1 ~\text{ft} \over 12 ~\text{in} } + {1 \over 1500} } \nonumber \\ &=& 827.6 ~{ \text{Btu} \over \text{hr-ft}^2\text{-}^{\circ}\text{F} } \end{eqnarray} $$ $$ \dot{Q} = U_o ~A_o ~\Delta T_{lm} $$ $$ \begin{eqnarray} { \dot{Q} \over L } &=& { U_o ~A_o ~\Delta T_{lm} \over L } \nonumber \\ &=& U_o ~2 \pi ~r ~\Delta T_{lm} \nonumber \\ &=& \left( 827.6 ~{ \text{Btu} \over \text{hr-ft}^2\text{-}^{\circ}\text{F} } \right) (2 \pi) (0.375 ~\text{in}) \left({ 1 ~\text{ft} \over 12 ~\text{in} }\right) (232^{\circ}\text{F}) \nonumber \\ &=& 37,000 ~{ \text{Btu} \over \text{hr-ft} } \end{eqnarray} $$


⟸ Previous Page
Next Page ⟹