Convection Heat Transfer

This page provides the chapter on convection heat transfer from the "DOE Fundamentals Handbook: Thermodynamics, Heat Transfer, and Fluid Flow," DOE-HDBK-1012/2-92, U.S. Department of Energy, June 1992.

Other related chapters from the "DOE Fundamentals Handbook: Thermodynamics, Heat Transfer, and Fluid Flow" can be seen to the right.

DOE Handbook: Heat Transfer

Convection Heat Transfer

Heat transfer by the motion and mixing of the molecules of a liquid or gas is called convection.

Convection

Convection involves the transfer of heat by the motion and mixing of "macroscopic" portions of a fluid (that is, the flow of a fluid past a solid boundary). The term natural convection is used if this motion and mixing is caused by density variations resulting from temperature differences within the fluid. The term forced convection is used if this motion and mixing is caused by an outside force, such as a pump. The transfer of heat from a hot water radiator to a room is an example of heat transfer by natural convection. The transfer of heat from the surface of a heat exchanger to the bulk of a fluid being pumped through the heat exchanger is an example of forced convection.

Heat transfer by convection is more difficult to analyze than heat transfer by conduction because no single property of the heat transfer medium, such as thermal conductivity, can be defined to describe the mechanism. Heat transfer by convection varies from situation to situation (upon the fluid flow conditions), and it is frequently coupled with the mode of fluid flow. In practice, analysis of heat transfer by convection is treated empirically (by direct observation).

Convection heat transfer is treated empirically because of the factors that affect the stagnant film thickness:

Convection involves the transfer of heat between a surface at a given temperature (T_s) and fluid at a bulk temperature (T_b). The exact definition of the bulk temperature (T_b) varies depending on the details of the situation. For flow adjacent to a hot or cold surface, T_b is the temperature of the fluid "far" from the surface. For boiling or condensation, T_b is the saturation temperature of the fluid. For flow in a pipe, T_b is the average temperature measured at a particular crosssection of the pipe.

The basic relationship for heat transfer by convection has the same form as that for heat transfer by conduction:

$$ \dot{Q} = h ~A ~\Delta T $$

(2-9)

where:

$ \dot{Q} $	=	rate of heat transfer (Btu/hr)
h	=	convective heat transfer coefficient (Btu/hr-ft²-°F)
A	=	surface area for heat transfer (ft²)
ΔT	=	temperature difference (°F)

The convective heat transfer coefficient (h) is dependent upon the physical properties of the fluid and the physical situation. Typically, the convective heat transfer coefficient for laminar flow is relatively low compared to the convective heat transfer coefficient for turbulent flow. This is due to turbulent flow having a thinner stagnant fluid film layer on the heat transfer surface. Values of h have been measured and tabulated for the commonly encountered fluids and flow situations occurring during heat transfer by convection.

Example:

A 22 foot uninsulated steam line crosses a room. The outer diameter of the steam line is 18 in. and the outer surface temperature is 280°F. The convective heat transfer coefficient for the air is 18 Btu/hr-ft²-°F. Calculate the heat transfer rate from the pipe into the room if the room temperature is 72°F.

Solution:

$$ \begin{eqnarray} \dot{Q} &=& h ~A ~\Delta T \nonumber \\ &=& h ~(2 \pi ~r ~L) ~\Delta T \nonumber \\ &=& \left( 18 ~{\text{Btu} \over \text{hr-ft-}^{\circ}\text{F}} \right) \left[ 2 (3.14) (0.75 ~\text{ft}) (22 ~\text{ft}) \right] (280^{\circ}\text{F} - 72^{\circ}\text{F}) \nonumber \\ &=& 3.88 \times 10^5 ~{ \text{Btu} \over \text{hr} } \end{eqnarray} $$

Many applications involving convective heat transfer take place within pipes, tubes, or some similar cylindrical device. In such circumstances, the surface area of heat transfer normally given in the convection equation ( $ \dot{Q} = h ~A ~\Delta T $ ) varies as heat passes through the cylinder. In addition, the temperature difference existing between the inside and the outside of the pipe, as well as the temperature differences along the pipe, necessitates the use of some average temperature value in order to analyze the problem. This average temperature difference is called the log mean temperature difference (LMTD), described earlier.

It is the temperature difference at one end of the heat exchanger minus the temperature difference at the other end of the heat exchanger, divided by the natural logarithm of the ratio of these two temperature differences. The above definition for LMTD involves two important assumptions: (1) the fluid specific heats do not vary significantly with temperature, and (2) the convection heat transfer coefficients are relatively constant throughout the heat exchanger.

Overall Heat Transfer Coefficient

Many of the heat transfer processes encountered in nuclear facilities involve a combination of both conduction and convection. For example, heat transfer in a steam generator involves convection from the bulk of the reactor coolant to the steam generator inner tube surface, conduction through the tube wall, and convection from the outer tube surface to the secondary side fluid.

In cases of combined heat transfer for a heat exchanger, there are two values for h. There is the convective heat transfer coefficient (h) for the fluid film inside the tubes and a convective heat transfer coefficient for the fluid film outside the tubes. The thermal conductivity (k) and thickness (Δx) of the tube wall must also be accounted for. An additional term (U_o), called the overall heat transfer coefficient, must be used instead. It is common practice to relate the total rate of heat transfer ($ \dot{Q} $) to the cross-sectional area for heat transfer (A_o) and the overall heat transfer coefficient (U_o). The relationship of the overall heat transfer coefficient to the individual conduction and convection terms is shown in Figure 6.

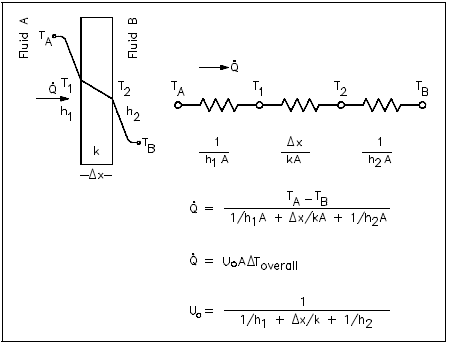
Figure 6: Overall Heat Transfer Coefficient

Recalling Equation 2-3:

$$ \dot{Q} = U_o ~A_o ~\Delta T_o $$

where U_o is defined in Figure 6.

An example of this concept applied to cylindrical geometry is illustrated by Figure 7, which shows a typical combined heat transfer situation.

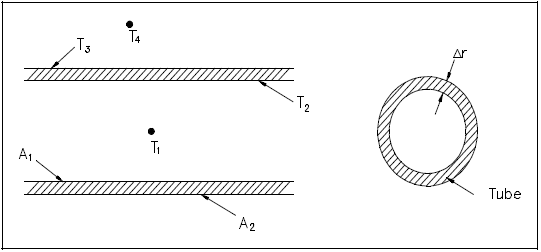
Using the figure representing flow in a pipe, heat transfer by convection occurs between temperatures T₁ and T₂; heat transfer by conduction occurs between temperatures T₂ and T₃; and heat transfer occurs by convection between temperatures T₃ and T₄. Thus, there are three processes involved. Each has an associated heat transfer coefficient, cross-sectional area for heat transfer, and temperature difference. The basic relationships for these three processes can be expressed using Equations 2-5 and 2-9.

$$ \dot{Q} = h_1 ~A_1 ~(T_1 - T_2) $$ $$ \dot{Q} = {k \over \Delta r} ~A_{lm} ~(T_2 - T_3) $$ $$ \dot{Q} = h_2 ~A_2 ~(T_3 - T_4) $$

ΔT_o can be expressed as the sum of the ΔT of the three individual processes.

ΔT_o = (T₁ − T₂) + (T₂ − T₃) + (T₃ − T₄)

If the basic relationship for each process is solved for its associated temperature difference and substituted into the expression for ΔT_o above, the following relationship results.

$$ \Delta T_o = \dot{Q} \left( {1 \over h_1 A_1} + { \Delta r \over k ~A_{lm} } + {1 \over h_2 A_2} \right) $$

This relationship can be modified by selecting a reference cross-sectional area A_o.

$$ \Delta T_o = { \dot{Q} \over A_o } \left( {A_o \over h_1 A_1} + { \Delta r ~A_o \over k ~A_{lm} } + {A_o \over h_2 A_2} \right) $$

Solving for $ \dot{Q} $ results in an equation in the form $ \dot{Q} = U_o ~A_o ~\Delta T_o $.

$$ \dot{Q} = { 1 \over \left( {A_o \over h_1 A_1} + { \Delta r ~A_o \over k ~A_{lm} } + {A_o \over h_2 A_2} \right) } ~A_o ~\Delta T_o $$

where:

$$ U_o = { 1 \over \left( {A_o \over h_1 A_1} + { \Delta r ~A_o \over k ~A_{lm} } + {A_o \over h_2 A_2} \right) } $$

Equation 2-10 for the overall heat transfer coefficient in cylindrical geometry is relatively difficult to work with. The equation can be simplified without losing much accuracy if the tube that is being analyzed is thin-walled, that is the tube wall thickness is small compared to the tube diameter. For a thin-walled tube, the inner surface area (A₁), outer surface area (A₂), and log mean surface area (A_lm), are all very close to being equal. Assuming that A₁, A₂, and A_lm are equal to each other and also equal to A_o allows us to cancel out all the area terms in the denominator of Equation 2-11.

This results in a much simpler expression that is similar to the one developed for a flat plate heat exchanger in Figure 6.

$$ U_o = { 1 \over {1 \over h_1} + { \Delta r \over k } + {1 \over h_2} } $$

(2-11)

The convection heat transfer process is strongly dependent upon the properties of the fluid being considered. Correspondingly, the convective heat transfer coefficient (h), the overall coefficient (U_o), and the other fluid properties may vary substantially for the fluid if it experiences a large temperature change during its path through the convective heat transfer device. This is especially true if the fluid's properties are strongly temperature dependent. Under such circumstances, the temperature at which the properties are "looked-up" must be some type of average value, rather than using either the inlet or outlet temperature value.

For internal flow, the bulk or average value of temperature is obtained analytically through the use of conservation of energy. For external flow, an average film temperature is normally calculated, which is an average of the free stream temperature and the solid surface temperature. In any case, an average value of temperature is used to obtain the fluid properties to be used in the heat transfer problem. The following example shows the use of such principles by solving a convective heat transfer problem in which the bulk temperature is calculated.

Convection Heat Transfer

Example:

A flat wall is exposed to the environment. The wall is covered with a layer of insulation 1 in. thick whose thermal conductivity is 0.8 Btu/hr-ft-°F. The temperature of the wall on the inside of the insulation is 600°F. The wall loses heat to the environment by convection on the surface of the insulation. The average value of the convection heat transfer coefficient on the insulation surface is 950 Btu/hr-ft²-°F. Compute the bulk temperature of the environment (T_b) if the outer surface of the insulation does not exceed 105°F.

Solution:

Find heat flux ($ \dot{Q}'' $) through the insulation.
$$ \dot{Q} = k ~A \left({ \Delta T \over \Delta x }\right) $$ $$ \begin{eqnarray} { \dot{Q} \over A } &=& 0.8 ~{\text{Btu} \over \text{hr-ft-}^{\circ}\text{F}} \left({ 600^{\circ}\text{F} - 105^{\circ}\text{F} \over 1 ~\text{in} ~{ 1 ~\text{ft} \over 12 ~\text{in} } }\right) \nonumber \\ &=& 4752 ~{ \text{Btu} \over \text{hr-ft}^2 } \end{eqnarray} $$
Find the bulk temperature of the environment.
$$ \begin{eqnarray} \dot{Q} &=& h ~A ~(T_{ins} - T_b) \nonumber \\ (T_{ins} - T_b) &=& { \dot{Q} \over h ~A } \nonumber \\ T_b &=& T_{ins} - { \dot{Q}'' \over h } \nonumber \\ T_b &=& 105^{\circ}\text{F} - { 4752 ~{ \text{Btu} \over \text{hr-ft}^2 } \over 950 ~{\text{Btu} \over \text{hr-ft-}^{\circ}\text{F}} } \nonumber \\ T_b &=& 100^{\circ}\text{F} \end{eqnarray} $$

⟸ Previous Page

Next Page ⟹

\( \dot{Q} \)	=	rate of heat transfer (Btu/hr)
h	=	convective heat transfer coefficient (Btu/hr-ft²-°F)
A	=	surface area for heat transfer (ft²)
ΔT	=	temperature difference (°F)