Conduction Heat Transfer

This page provides the chapter on conduction heat transfer from the "DOE Fundamentals Handbook: Thermodynamics, Heat Transfer, and Fluid Flow," DOE-HDBK-1012/2-92, U.S. Department of Energy, June 1992.

Other related chapters from the "DOE Fundamentals Handbook: Thermodynamics, Heat Transfer, and Fluid Flow" can be seen to the right.

DOE Handbook: Heat Transfer

Conduction Heat Transfer

Conduction heat transfer is the transfer of thermal energy by interactions between adjacent atoms and molecules of a solid.

Conduction

Conduction involves the transfer of heat by the interaction between adjacent molecules of a material. Heat transfer by conduction is dependent upon the driving "force" of temperature difference and the resistance to heat transfer. The resistance to heat transfer is dependent upon the nature and dimensions of the heat transfer medium. All heat transfer problems involve the temperature difference, the geometry, and the physical properties of the object being studied.

In conduction heat transfer problems, the object being studied is usually a solid. Convection problems involve a fluid medium. Radiation heat transfer problems involve either solid or fluid surfaces, separated by a gas, vapor, or vacuum. There are several ways to correlate the geometry, physical properties, and temperature difference of an object with the rate of heat transfer through the object. In conduction heat transfer, the most common means of correlation is through Fourier's Law of Conduction. The law, in its equation form, is used most often in its rectangular or cylindrical form (pipes and cylinders), both of which are presented below.

Rectangular

$$ \dot{Q} = k ~A \left({ \Delta T \over \Delta x }\right) $$

(2-4)

Cylindrical

$$ \dot{Q} = k ~A \left({ \Delta T \over \Delta r }\right) $$

(2-5)

where:

$ \dot{Q} $	=	rate of heat transfer (Btu/hr)
A	=	cross-sectional area of heat transfer (ft²)
Δx	=	thickness of slab (ft)
Δr	=	thickness of cylindrical wall (ft)
ΔT	=	temperature difference (°F)
k	=	thermal conductivity of slab (Btu/ft-hr-°F)

The use of Equations 2-4 and 2-5 in determining the amount of heat transferred by conduction is demonstrated in the following examples.

Conduction-Rectangular Coordinates

Example:

1000 Btu/hr is conducted through a section of insulating material shown in Figure 1 that measures 1 ft² in cross-sectional area. The thickness is 1 in. and the thermal conductivity is 0.12 Btu/hr-ft-°F. Compute the temperature difference across the material.

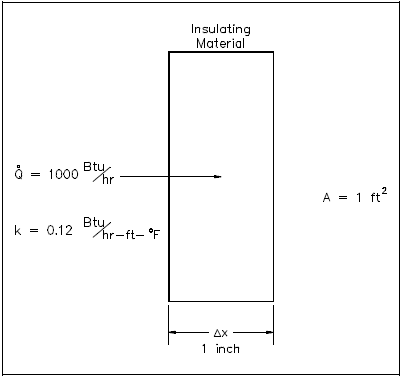
Solution:

Using Equation 2-4:

$$ \dot{Q} = k ~A \left({ \Delta T \over \Delta x }\right) $$

Solving for ΔT:

$$ \begin{eqnarray} \Delta T &=& \dot{Q} \left({ \Delta x \over k ~A }\right) \nonumber \\ &=& { \left({ 1000 ~{\text{Btu} \over \text{hr}} }\right) \left({1 \over 12} ~\text{ft}\right) \over \left({ 0.12 ~{\text{Btu} \over \text{hr-ft-}^{\circ}\text{F}} }\right) (1 ~\text{ft}^2) } \nonumber \\ \Delta T &=& 694^{\circ}F \end{eqnarray} $$

Example:

A concrete floor with a conductivity of 0.8 Btu/hr-ft-°F measures 30 ft by 40 ft with a thickness of 4 inches. The floor has a surface temperature of 70°F and the temperature beneath it is 60°F. What is the heat flux and the heat transfer rate through the floor?

Solution:

Using Equations 2-1 and 2-4:

$$ \begin{eqnarray} \dot{Q}'' &=& { \dot{Q} \over A } = k \left({ \Delta T \over \Delta x }\right) \nonumber \\ &=& \left({ 0.8 ~{\text{Btu} \over \text{hr-ft-}^{\circ}\text{F}} }\right) \left({ 10^{\circ}\text{F} \over 0.333 ~\text{ft} }\right) \nonumber \\ &=& 24 ~{ \text{Btu} \over \text{hr-ft}^2 } \end{eqnarray} $$

Using Equation 2-3:

$$ \begin{eqnarray} \dot{Q} &=& k ~A \left({ \Delta T \over \Delta x }\right) = \dot{Q}'' A \nonumber \\ &=& \left(24 ~{ \text{Btu} \over \text{hr-ft}^2 }\right) (1200 ~\text{ft}^2) \nonumber \\ &=& 28,800 ~{\text{Btu} \over \text{hr}} \end{eqnarray} $$

Equivalent Resistance Method

It is possible to compare heat transfer to current flow in electrical circuits. The heat transfer rate may be considered as a current flow and the combination of thermal conductivity, thickness of material, and area as a resistance to this flow. The temperature difference is the potential or driving function for the heat flow, resulting in the Fourier equation being written in a form similar to Ohm's Law of Electrical Circuit Theory. If the thermal resistance term Δx/k is written as a resistance term where the resistance is the reciprocal of the thermal conductivity divided by the thickness of the material, the result is the conduction equation being analogous to electrical systems or networks. The electrical analogy may be used to solve complex problems involving both series and parallel thermal resistances. The student is referred to Figure 2, showing the equivalent resistance circuit. A typical conduction problem in its analogous electrical form is given in the following example, where the "electrical" Fourier equation may be written as follows.

$$ \dot{Q}'' = { \Delta T \over R_{th} } $$

(2-6)

where:

$ \dot{Q}'' $	=	Heat Flux ($ \dot{Q}/A $) (Btu/hr-ft²)
ΔT	=	Temperature Difference (°F)
R_th	=	Thermal Resistance (Δx/k) (hr-ft²-°F/Btu)

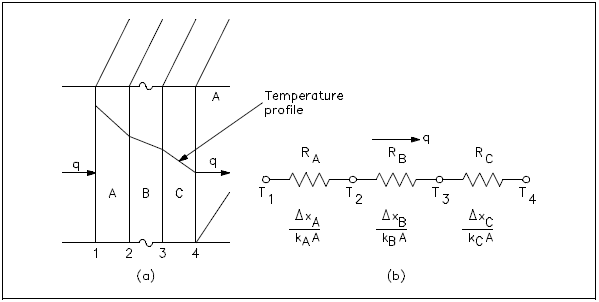
Electrical Analogy

Example:

A composite protective wall is formed of a 1 in. copper plate, a 1/8 in. layer of asbestos, and a 2 in. layer of fiberglass. The thermal conductivities of the materials in units of Btu/hr-ft-°F are as follows: k_Cu = 240, k_asb = 0.048, and k_fib = 0.022. The overall temperature difference across the wall is 500°F. Calculate the thermal resistance of each layer of the wall and the heat transfer rate per unit area (heat flux) through the composite structure.

Solution:

$$ \begin{eqnarray} R_{Cu} &=& { \Delta x_{Cu} \over k_{Cu} } \nonumber \\ &=& { 1 ~\text{in} \left({ 1 ~\text{ft} \over 12 ~\text{in} }\right) \over 240 ~{\text{Btu} \over \text{hr-ft-}^{\circ}\text{F}} } \nonumber \\ &=& 0.000347 ~{\text{hr-ft}^2\text{-}^{\circ}\text{F} \over \text{Btu}} \end{eqnarray} $$

$$ \begin{eqnarray} R_{asb} &=& { \Delta x_{asb} \over k_{asb} } \nonumber \\ &=& { 0.125 ~\text{in} \left({ 1 ~\text{ft} \over 12 ~\text{in} }\right) \over 0.048 ~{\text{Btu} \over \text{hr-ft-}^{\circ}\text{F}} } \nonumber \\ &=& 0.2170 ~{\text{hr-ft}^2\text{-}^{\circ}\text{F} \over \text{Btu}} \end{eqnarray} $$

$$ \begin{eqnarray} R_{fib} &=& { \Delta x_{fib} \over k_{fib} } \nonumber \\ &=& { 2 ~\text{in} \left({ 1 ~\text{ft} \over 12 ~\text{in} }\right) \over 0.022 ~{\text{Btu} \over \text{hr-ft-}^{\circ}\text{F}} } \nonumber \\ &=& 7.5758 ~{\text{hr-ft}^2\text{-}^{\circ}\text{F} \over \text{Btu}} \end{eqnarray} $$

$$ \begin{eqnarray} { \dot{Q} \over A } &=& { ( T_i - T_o ) \over ( R_{Cu} + R_{asb} + R_{fib} ) } \nonumber \\ &=& { 500^{\circ}\text{F} \over (0.000347 0.2170 + 7.5758) ~{\text{hr-ft}^2\text{-}^{\circ}\text{F} \over \text{Btu}} } \nonumber \\ &=& 64.2 ~{\text{Btu} \over \text{hr-ft}^2} \end{eqnarray} $$

Conduction-Cylindrical Coordinates

Heat transfer across a rectangular solid is the most direct application of Fourier's law. Heat transfer across a pipe or heat exchanger tube wall is more complicated to evaluate. Across a cylindrical wall, the heat transfer surface area is continually increasing or decreasing. Figure 3 is a cross-sectional view of a pipe constructed of a homogeneous material.

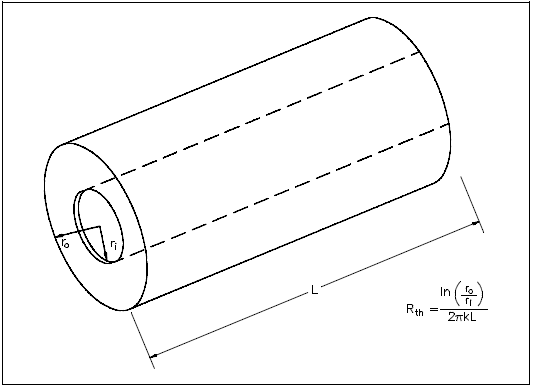
Figure 3: Cross-sectional Surface Area of a Cylindrical Pipe

The surface area (A) for transferring heat through the pipe (neglecting the pipe ends) is directly proportional to the radius (r) of the pipe and the length (L) of the pipe.

A = 2πrL

As the radius increases from the inner wall to the outer wall, the heat transfer area increases.

The development of an equation evaluating heat transfer through an object with cylindrical geometry begins with Fourier's law Equation 2-5.

$$ \dot{Q} = k ~A \left({ \Delta T \over \Delta r }\right) $$

From the discussion above, it is seen that no simple expression for area is accurate. Neither the area of the inner surface nor the area of the outer surface alone can be used in the equation. For a problem involving cylindrical geometry, it is necessary to define a log mean cross-sectional area (A_lm).

$$ A_{lm} = { A_{outer} - A_{inner} \over \ln \left({ A_{outer} \over A_{inner} }\right) } $$

(2-7)

Substituting the expression 2πrL for area in Equation 2-7 allows the log mean area to be calculated from the inner and outer radius without first calculating the inner and outer area.

$$ \begin{eqnarray} A_{lm} &=& { 2 \pi ~r_{outer} L - 2 \pi ~r_{inner} L \over \ln \left({ 2 \pi ~r_{outer} L \over 2 \pi ~r_{inner} L }\right) } \nonumber \\ &=& 2 \pi ~L \left({ r_{outer} - r_{inner} \over \ln{ r_{outer} \over r_{inner} } }\right) \end{eqnarray} $$

This expression for log mean area can be inserted into Equation 2-5, allowing us to calculate the heat transfer rate for cylindrical geometries.

$$ \begin{eqnarray} \dot{Q} &=& k ~A_{lm} \left({ \Delta T \over \Delta r }\right) \nonumber \\ &=& k \left[ 2 \pi ~L \left({ r_o - r_i \over \ln{ r_o \over r_i } }\right) \right] \left({ T_o - T_i \over r_o - r_i }\right) \nonumber \\ \dot{Q} &=& { 2 \pi ~k ~L ~(\Delta T) \over \ln (r_o / r_i) } \end{eqnarray} $$

(2-8)

where:

L	=	length of pipe (ft)
r_i	=	inside pipe radius (ft)
r_o	=	outside pipe radius (ft)

Example:

A stainless steel pipe with a length of 35 ft has an inner diameter of 0.92 ft and an outer diameter of 1.08 ft. The temperature of the inner surface of the pipe is 122°F and the temperature of the outer surface is 118°F. The thermal conductivity of the stainless steel is 108 Btu/hr-ft-°F.

Calculate the heat transfer rate through the pipe.

Calculate the heat flux at the outer surface of the pipe.

Solution:

$$ \begin{eqnarray} \dot{Q} &=& { 2 \pi ~k ~L ~(T_h - T_c) \over \ln (r_o / r_i) } \nonumber \\ &=& { 6.28 \left( 108 ~{\text{Btu} \over \text{hr-ft-}^{\circ}\text{F}} \right) (35 ~\text{ft}) (122^{\circ}\text{F} - 118^{\circ}\text{F}) \over \ln { 0.54 ~\text{ft} \over 0.46 ~\text{ft} } } \nonumber \\ &=& 5.92 \times 10^5 ~{ \text{Btu} \over \text{hr} } \end{eqnarray} $$ $$ \begin{eqnarray} \dot{Q}'' &=& { \dot{Q} \over A } \nonumber \\ &=& { \dot{Q} \over 2 \pi ~r_o ~L } \nonumber \\ &=& { 5.92 \times 10^5 ~{ \text{Btu} \over \text{hr} } \over 2 (3.14) (0.54 ~\text{ft}) (35 ~\text{ft}) } \nonumber \\ &=& 4985 ~{ \text{Btu} \over \text{hr-ft}^2 } \end{eqnarray} $$

Example:

A 10 ft length of pipe with an inner radius of 1 in and an outer radius of 1.25 in has an outer surface temperature of 250°F. The heat transfer rate is 30,000 Btu/hr. Find the interior surface temperature. Assume k = 25 Btu/hr-ft-°F.

Solution:

$$ \dot{Q} = { 2 \pi ~k ~L ~(T_h - T_c) \over \ln (r_o / r_i) } $$

Solving for T_h:

$$ \begin{eqnarray} T_h &=& { \dot{Q} ~\ln (r_o / r_i) \over 2 \pi ~k ~L } + T_c \nonumber \\ &=& { \left( 30,000 ~{ \text{Btu} \over \text{hr} } \right) \left( \ln { 1.25 ~\text{in} \over 1 ~\text{in} } \right) \over 2 (3.14) \left(25 ~{\text{Btu} \over \text{hr-ft-}^{\circ}\text{F}} \right) (10 ~\text{ft}) } + 250^{\circ}\text{F} \nonumber \\ &=& 254^{\circ}\text{F} \end{eqnarray} $$

The evaluation of heat transfer through a cylindrical wall can be extended to include a composite body composed of several concentric, cylindrical layers, as shown in Figure 4.

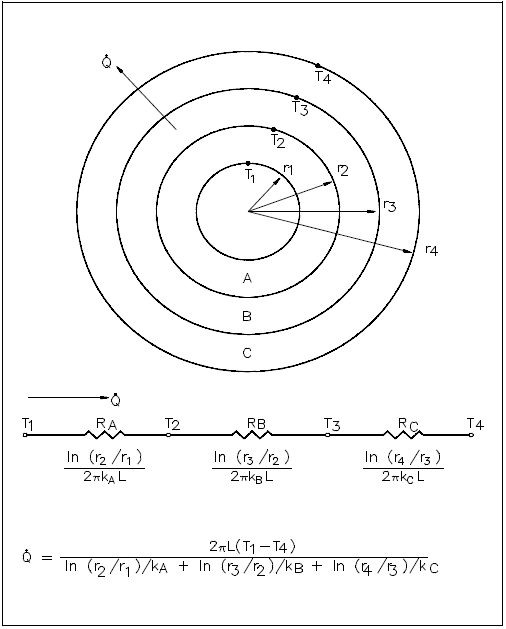
Example:

A thick-walled nuclear coolant pipe (k_s = 12.5 Btu/hr-ft-°F) with 10 in. inside diameter (ID) and 12 in. outside diameter (OD) is covered with a 3 in. layer of asbestos insulation (k_a = 0.14 Btu/hr-ft-°F) as shown in Figure 5. If the inside wall temperature of the pipe is maintained at 550°F, calculate the heat loss per foot of length. The outside temperature is 100°F.

Solution:

$$ \begin{eqnarray} { \dot{Q} \over L } &=& { 2 \pi ~(T_{in} - T_o) \over \left[ { \ln (r_2 / r_1) \over k_s } + { \ln (r_3 / r_2) \over k_a } \right] } \nonumber \\ &=& { 2 \pi ~(550^{\circ}\text{F} - 100^{\circ}\text{F}) \over \left[ { \ln \left({ 6 ~\text{in} \over 5 ~\text{in} }\right) \over 12.5 ~{\text{Btu} \over \text{hr-ft-}^{\circ}\text{F}} } + { \ln \left({ 9 ~\text{in} \over 6 ~\text{in} }\right) \over 0.14 ~{\text{Btu} \over \text{hr-ft-}^{\circ}\text{F}} } \right] } \nonumber \\ &=& 971 ~{ \text{Btu} \over \text{hr-ft} } \end{eqnarray} $$

⟸ Previous Page

Next Page ⟹

\( \dot{Q} \)	=	rate of heat transfer (Btu/hr)
A	=	cross-sectional area of heat transfer (ft²)
Δx	=	thickness of slab (ft)
Δr	=	thickness of cylindrical wall (ft)
ΔT	=	temperature difference (°F)
k	=	thermal conductivity of slab (Btu/ft-hr-°F)

\( \dot{Q}'' \)	=	Heat Flux (\( \dot{Q}/A \)) (Btu/hr-ft²)
ΔT	=	Temperature Difference (°F)
R_th	=	Thermal Resistance (Δx/k) (hr-ft²-°F/Btu)