Guideline for Bolted Joint Design and Analysis

This page provides details on the design and analysis of bolted joints. This source of this page is Brown et al., "Guideline for Bolted Joint Design and Analysis: Version 1.0," Sandia Report SAND2008-0371, Sandia National Laboratories, 2008.

Abstract

This document provides general guidance for the design and analysis of bolted joint connections. An overview of the current methods used to analyze bolted joint connections is given. Several methods for the design and analysis of bolted joint connections are presented. Guidance is provided for general bolted joint design, computation of preload uncertainty and preload loss, and the calculation of the bolted joint factor of safety. Axial loads, shear loads, thermal loads, and thread tear out are used in factor of safety calculations. Additionally, limited guidance is provided for fatigue considerations.

1 Introduction

The purpose of this report is to document the current state of the art in bolted joint design and analysis and to provide guidance to engineers designing and analyzing bolted connections. There is no one right answer or way to approach all the cases. In many cases, additional work will be needed to assess the quality of current practices and provide guidance. General information, suggestions, and guidelines are provided here but ultimately the engineer must use his/her judgment on which approach is applicable and the level of detailed analysis required.

The basic philosophy is to use a staged approach. The first stage is based on idealized models to provide an initial estimate useful for design. If the joint is simple enough and the margins are large enough, this may be all that is required. In contrast, a complicated joint or one with small margins may require additional analysis. This can range from a relatively simple axisymmetric linear elastic finite element model to a fully nonlinear three dimensional finite element model incorporating geometric nonlinearities and frictional contact.

For version 1.0 of this document, the primary focus is on how to evaluate factors of safety for a single bolt of a bolted joint once the axial and shear loads on it are known. The load can be obtained from either analytic models or finite element analyses. Analytic methods for determining the loads on a given bolt of a joint can be found in Shigley [16] or other mechanical engineering texts.

2 Nomenclature

This section provides a comprehensive list of symbols used in equations and figures in subsequent sections. Section 2.1 contains two tables, one for variables defined using the standard alphabet and a second table for variables defined using the Greek alphabet.

2.1 Variables Menu

The following two tables list variables used throughout this document. The column listing units is intended to provide the user with guidance regarding units. Units are given in terms of length (L), force (F), radians (rad) and temperature (T). nd is used to denote non-dimensional quantities. Any consistent set of units may be used.

Where possible, the description identifies a figure or equation that further defines the parameter. Subscripts not specifically identified in these tables will be addressed during discussions in the appropriate text.

Table 1: List of Symbols
Symbol	Units	Description
A	L²	General symbol for area
A_b	L²	Area of bolt cross-section.
A_t	L²	Tensile Area of a bolt used for thread tear out calculations (See Section 8.1)
C	nd	Integrated joint stiffness constant. (Equation 26)
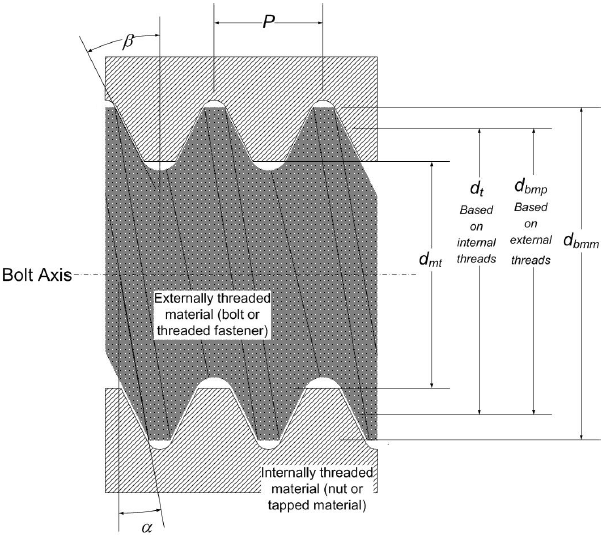
D_B	L	Equivalent diameter of torque bearing surfaces (Equation 53)
d₂	L	Effective diameter of internal (nut) threads
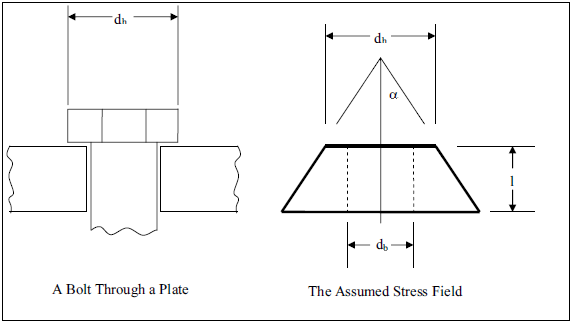
d_b	L	Nominal bolt diameter and externally threaded material (bolt) major diameter for thread tear out (Figure 2)
d_bmm	L	Externally threaded material (bolt) minimum major diameter
d_bmp	L	Externally threaded material (bolt) minimum pitch diameter (Figure 2)
d_c	L	Diameter of the clearance hole(s) (Figure 1). Physically, this parameter could be different for every clamped layer but for the equations presented in this document, it is assumed to be the same value for all layers.
d_h	L	Diameter of the load bearing area between the bolt head and the clamped material (Figure 1)
D_c	L	The effective diameter of an assumed cylindrical stress geometry in the clamped material. Used in Pulling's method (Equation 13)
D_j	L	Diameter of a bolted joint. Used in Bickford method
d_mt	L	Internally threaded material (nut) maximum minor diameter (Figure 2)
d_t	L	Internally threaded material (nut) maximum pitch diameter (Figure 2)
E	F/L²	General symbol for Young's modulus of a material. Unless identified below, subscripts will be identified in the text.
E_b	F/L²	Young's modulus for bolt material
E_eff	F/L²	Effective Young's modulus for a clamped stack consisting of multiple materials
E_ls	F/L²	Young's modulus for the less stiff (ls) material in a two material bolted joint.
E_ms	F/L²	Young's modulus for the more stiff (ms) material in a two material bolted joint.
F	F	The external axial load applied to separate clamped materials
F_b	F	That portion of F taken up by the bolt
F_m	F	That portion of F taken up by the clamped material
FOS	nd	Factor of safety
F_p	F	Bolt preload
F_pr	F	Bolt proof load. This is the manufacturer specified axial load the bolt must withstand without permanent set.
I	L⁴	Moment of inertia
J_e	nd	Factor used in the computation of thread tear out
K	nd	Nut factor. (Equation 1)
K_e	L	Length of engaged threads needed to avoid tear-out in using high tensile strength bolts
k	F/L	General symbol for stiffness of a bolt, clamped material or overall joint. Unless identified below, subscripts will be identified in the text.
k_b	F/L	Stiffness of the bolt
k_j	F/L	Stiffness of the joint
k_m	F/L	Stiffness of the clamped material
L_i	L	Length of individual component in a bolted joint.
L_e	L	Minimum length of engagement of a threaded joint to prevent thread tear out
l	L	Thickness of clamped material. Also used as the length of bolt in the joint.
l_eff	L	Effective length of engagement between a bolt and a tapped threaded material (as opposed to a nut)
l_ls	L	Thickness of the less stiff (lower Young's modulus) clamped material
l_ms	L	Thickness of the more stiff (higher Young's modulus) clamped material
MOS	nd	Margin of safety
N	nd	Ratio of length of less stiff material to total length of the joint (Equation 21)
n_i	nd	Number of cycles a joint experiences at the i^th stress level
N_i	nd	Expected cycles to failure at the i^th stress level
P	L	Thread Pitch (Figure 2)
Q	nd	Ratio of of an assumed cylindrical stress field to the bolt diameter (typically d_b).
q_i	nd	Ratio of the clearance hole diameter (d_c) to the bolt diameter (d_b)
R_e	L	Effective radius to which the torque is applied (average of R_o and R_i).
R_i	L	Analyst's estimate of inner radius of the torqued element (often equal to d_b/2 if clearances are ignored)
R_o	L	Analyst's estimate of outer radius of the torqued element (often equal to d_h/2)
R_s	L	Factor relating total shear load on a bolt to the shear strength of that bolt
R_t	nd	Factor relating total tensile load on a bolt to the tensile strength of the bolt
S_u	F/L²	Ultimate tensile strength of a material
S_y	F/L²	Yield strength of a material
T_o	F·L	Axial torque applied to a bolt
T, ΔT	T	Temperature or temperature change
X, Y	nd	Exponents used in the calculation margin of safety calculations for combining axial and shear loads for a bolt. (Equation 50)
x_G	nd	Dimensionless joint geometry parameter, or aspect ratio, used in the DMP method (equation 24)

Table 2: Greek Symbols
Symbol	Units	Description
α	rad	Thread helix angle (Figure 2) and the frustum angle for Shigley's method.
α'	rad	Computed angle based on β and α. (Equation 54)
α_L	T^-1	Coefficient of linear thermal expansion
β	rad	Thread half angle (Figure 2)
δ	L	Total elongation of the bolt
μ_B	nd	Coefficient of friction between bearing surfaces
μ_t	nd	Coefficient of friction between threads
σ	F/L²	Applied tensile or compressive stress in a stress field. Usually subscripted. Subscripts will be described in the text.
τ	F/L²	Applied shear stress in a stress field. Usually subscripted. Subscripts will be described in the text.

Figure 1 contains a cross section of a typical through-bolted joint. It consists of a bolt, two washers, two materials, and a nut. For the purposes of this version of the document, washers can either be considered part of the bolt or as individual layers of clamped material.

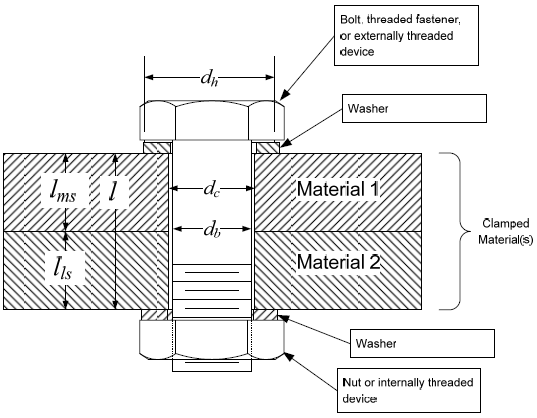
While this joint includes washers on both ends, many bolted joints do not use washers and the methodologies presented in this document apply to bolted joints with or without washers. A clearance between the bolt and the clamped materials can be accounted for, however, the methodologies presented here assume a single clearance that applies to all the layers. Figure 2 identifies important geometric parameters for a thread joint.

3 General Guidelines

The guidelines NASA [11] used for bolted joints on the space shuttle are generally applicable and are adopted here.

A preloaded joint must meet, as a minimum, the following three basic requirements:

The bolt must have adequate strength.
The joint must demonstrate a separation factor of safety at limit load. This generally means the joint must not separate at the maximum load to be applied to the joint.
The bolt must have adequate fracture and fatigue life.

Bolt strength is checked at maximum external load and maximum preload, and joint separation is checked at maximum external load and minimum preload. To do this, a conservative estimate of the maximum and minimum preloads must be made, so that no factors of safety are required for these preloads. Safety factors need only be applied to external loads.

4 Bolt Preload

A critical component of designing bolted joints is not only determining the number of bolts, the size of them, and the placement of them but also determining the appropriate preload for the bolt and the torque that must be applied to achieve the desired preload. There is no one right choice for the preload or torque. Many factors need to be considered when making this determination. A basic guideline given in the Machinery's Handbook [12] is to use 75% of the proof strength (or 75% of 85% of the material yield strength if the proof strength is not known) for removable fasteners and 90% of the proof strength for permanent fasteners. Things to consider include the tension in the bolt and therefore the clamping force, fatigue concerns (higher preload is generally preferable), how much torque can easily be applied without risking damaging another part if the tool slips while applying the load, etc.

The Machinery's Handbook [12] and the NASA guide [11] give estimates for the accuracy of bolt preload based on application method. The NASA guide states these uncertainties should be used for all small fasteners (defined as those less than 3/4"). The results are summarized in Table 3.

Table 3: Accuracy of Bolt Preload Based on Application Method
Method	Accuracy
Torque Wrench on Unlubricated Bolts [11]	± 35%
Torque Wrench on Cad-Plated Bolts [11]	± 30%
Torque Wrench on Lubricated Bolts [11]	± 25%
Preload Indicating Washer [11]	± 10%
Strain Gages [12]	± 1%
Computer Controlled Wrench (Below Yield) [12]	± 15%
Computer Controlled Wrench (Yield Sensing) [12]	± 8%
Bolt Elongation [11]	± 5%
Ultrasonic Sensing [11]	± 5%

A general relationship between applied torque, T, and the preload in the bolt, F_p, can be written in terms of the bolt diameter, d, and the "Nut Factor", K, as

T = K · d_b · F_P

(1)

Table 4 gives ranges for nut factors for a variety of materials and lubricants. The data is taken from the Standard Handbook of Machine Design [15]. Their data is based on multiple sources. As can be seen by examining the data, there can be large ranges of potential nut factors and as such, it is recommended in the Standard Handbook of Machine Design [15] to only use nut factors when approximate preload is sufficient for the design. For cases where strain gages can not be used, bolt extension can not be measured, load sensing washers can not be used, etc., there is no choice but use a nut factor. In these cases, any analysis should be done using a range of nut factors to bound the results. A low nut factor gives a higher preload and clamping force but puts the bolt closer to yield while a high nut factor gives a lower preload and clamping force but the capacity of the joint to resist external tensile loads has been reduced.

Table 4. Nut Factors for Various Lubricants
Lubricant	Nut Factor
Lubricant	Mean	Range
Cadmium Plating	0.194-0.246	0.153-0.328
Zinc Plate	0.332	0.262-0.398
Black Oxide	0.163-0.194	0.109-0.279
Baked on PTFE	0.092-0.112	0.064-0.142
Molydisulfide Paste	0.155	0.14-0.17
Machine Oil	0.21	0.20-0.225
Carnaba Wax (5% Emulsion)	0.148	0.12-0.165
60 Spindle Oil	0.22	0.21-0.23
As Received Steel Fasteners	0.20	0.158-0.267
Molydisulfide Grease	0.137	0.10-0.16
Phosphate and Oil	0.19	0.15-0.23
Plated Fasteners	0.15
Grease, Oil, or Wax	0.12

Additional information on nut factors can be found in Bickford [4] and the Machinery's Handbook [12]. A summary of analytic approaches to compute a nut factor are given in Appendix A. At this point, the recommended method is to use a pre-computed nut factor from Table 4 until the analytic methods are better understood, compared to the known methods, and confidence is gained in the accuracy of the method. The analytic methods seem to produce artificially large nut factors (which produce very small preloads for a given torque). This is something that will be looked at in follow-on work to the initial release of this report.

5 Analytic Modeling Approaches

All of the analytic approaches presented in this section implicitly assume an axisymmetic stress field. Any geometric or material effects that significantly violate this assumption make the approaches in this section invalid. This can include bolts very close together, bolts near a physical boundary (see section 5.4), non axisymmetric geometries, etc. If the bolted joint of interest does not meet these assumptions (and the additional assumptions of the approaches below) then it is recommended that a finite element analysis be used for the joint.

The general approach is to idealize a bolted joint into a pair of springs in parallel. One spring represents the bolt and other represents the clamped material. If an estimate can be obtained for the stiffness of the bolt (which is trivial) and the clamped material (which is difficult), then externally applied axial loads can be partitioned appropriately between the two and factors of safety can be computed to determine if the joint design is sufficient.

It is generally assumed that the clamped material can be viewed as a set of springs in series and an overall stiffness for the clamped material, k_m, can be computed as

$$ {1 \over k_m} = {1 \over k_1} + {1 \over k_2} + ... + {1 \over k_i} $$

(2)

where k_i is the stiffness of the i^th layer. The bolt stiffness, k_b, can be estimated in terms of the cross sectional area of the bolt, A_b, Young's modulus for the bolt, E_b, and the length of the bolt, L_b, as

$$ k_b = { A_b E_b \over L_b } $$

(3)

The total stiffness of the joint, k_j, can be computed (by assuming two springs in parallel) as

k_j = k_b + k_m

(4)

The remainder of this chapter is devoted to various methods of estimating the stiffness of the clamped material and comparing the various methods. It will be recommended that the FEA empirical models be used when they are applicable and to use Shigley's frustum approach for all other cases.

5.1 Cylindrical Stress Field Method (Q Factor)

In this method it is assumed the true 'barrel shaped' stress field can be approximated as a cylinder of diameter d_c (see Figure 3, d_c equals Qd). This was the original assumption made by Shigley in his first edition mechanical engineering design book [8] and is what is chosen by Bickford [4].

A factor, Q, is defined as the ratio between the actual bolt diameter and the idealized cylindrical stress field

Q = d_c / d

(5)

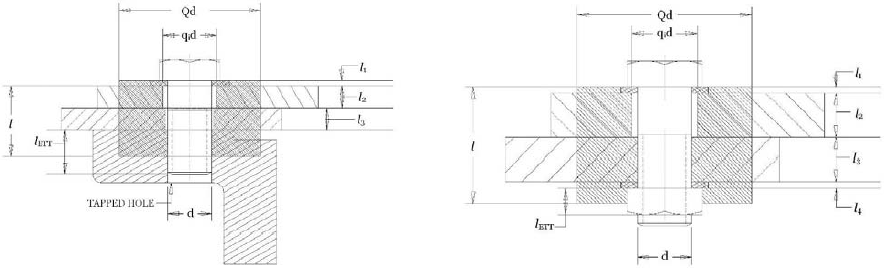
Figure 3. Q Factor Stress Distribution for 2 Geometries

By considering the layer as a one dimensional spring, the stiffness of the i^th layer can be computed as

$$ k_i = { A_i E_i \over L_i } $$

(6)

The area of the i^th layer can be computed, assuming the inner diameter is q_id_b (where q_i ≥ 1 and is used to allow for clearance between the clamped material and the bolt) and the outer diameter is Qd_b, as

$$ A_i = { \pi \over 4 } \left[ (Q d_b)^2 - (q_i d_b)^2 \right] = { \pi \over 4 } ~d_b^2 ~(Q^2 - q_i^2) $$

(7)

The addition of q_i is a logical extension to account for clearance holes that were included in the work of Pulling, et. al. [13] and is adopted here. The axial stiffness of the clamped material can be written as

$$ k_{axial} = { \pi ~d_b^2 \over 4 } \sum_{i} { E_i (Q^2 - q_i^2) \over L_i } $$

(8)

Pulling, et. al. [13], went on to define a bending stiffness for the clamped material using the same methodology. They assumed that the same material is loading in bending as was loaded axially. The approach is based on beam theory and as such they are assuming the ends (i.e. the edge of the assumed loaded material) are free (i.e. there is no rotation constraint posed by the material beyond that considered loaded). With these assumptions, the bending stiffness for each layer can be computed to be

$$ k_{bending.i} = { E_i I_i \over L_i } $$

(9)

The moment of inertia, I, for the i^th layer can be computed as

$$ I_i = { \pi \over 64 } \left[ (Q d_b)^4 - (q_i d_b)^4 \right] $$

(10)

Once again assuming each layer is represented by a spring in series, the bending stiffness of the clamped material can be computed as

$$ k_{bending} = { \pi ~d_b^4 \over 64 } \sum_{i} { E_i (Q^4 - q_i^4) \over L_i } $$

(11)

For the case of a bolted flange of a pipe with the bending applied to the neutral axis of the pipe, the actual load on the bolt will be more like an axial load and less like a bending load. There is an additional concern with this method because it is probable that the actual load on the bolt due to bending will be higher than what this theory predicts (i.e. this does not produce conservative results). This is a major concern and great care must be taken when considering bending loads on bolted joints with this method.

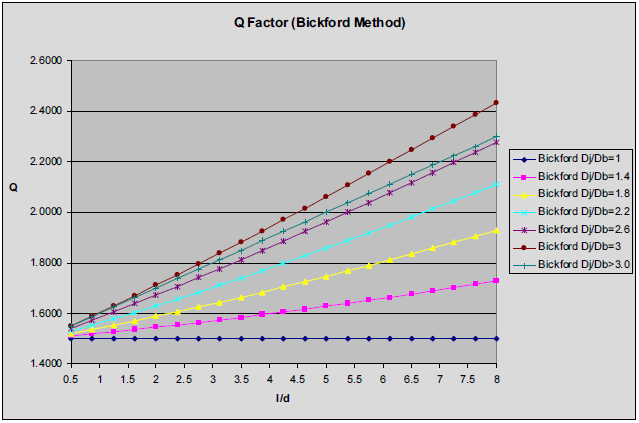
The original guideline put out by Pulling, et. al. [13] used a value of 3 for Q. This is the value Shigley used in the 1st edition of Mechanical Engineering Design. The accuracy of this method is highly dependent on the choice of Q. As can be seen, Q is squared (or raised to the 4th power for bending), and therefore any errors in Q are magnified. As will be shown by comparing the different methods in a later section, the value of Q is variable and depends on the geometry of the joint.

Bickford [4] noted that spheres, cylinders and frustums could all be used. He also chose to use a cylinder. He derived the same expressions for axial loading that were shown above (except he did not include qi to account for clearance) and provided the following guidance for Q (actually he provided guidance for the area of the cylinder which implies Q). His equations are modified here to account for qi so that it can be compared to the work of Pulling [13]. For the case where the bolt head diameter (or washer diameter) is greater than the joint "diameter" of the material being clamped, the entire area is used so

$$ A = { \pi \over 4 } \left[ D_J^{~2} - (q d_b)^2 \right] = { \pi \over 4 } \left[ (Q d_b)^2 - (q d_b)^2 \right] ~~\text{when}~~ d_h \ge D_J $$

(12)

where D_J is the diameter of the joint. This implies

$$ Q = { D_J \over d } ~~\text{when}~~ d_h \ge D_J $$

(13)

For the case where the joint "diameter" is greater than the diameter of the bolt head (or washer) but less than three times the diameter, the area that should be used is

$$ A = { \pi \over 4 } \left[ d_h^2 - (q d_b)^2 \right] + {\pi \over 8} \left( {D_J \over d_h} - 1 \right) \left( {d_h l \over 5} + {l^2 \over 100} \right) ~~\text{when}~~ d_h \lt D_J \le 3 d_h $$

(14)

The first term accounts for all the area under the bolt (or washer). The second term accounts for additional material based on the thickness, l, of the joint. This implies a Q factor of

$$ Q = {1 \over d} \sqrt{ d_h^2 + \left( {D_J \over d_h} - 1 \right) \left( {d_h l \over 10} + {l^2 \over 200} \right) } ~~\text{when}~~ d_h \lt D_J \le 3 d_h $$

(15)

For the case where the joint "diameter" is greater than three times the diameter the of the bolt (or washer), the area that should be used is

$$ A = {\pi \over 4} \left[ \left( d_h + {l \over 10} \right)^2 - (q d_b)^2 \right] ~~\text{when}~~ D_J \gt 3 d_h ~~\text{and}~~ l \le 8 d_h $$

(16)

Again it can be seen that the equation above accounts for the materials under the bolt plus additional material that is dependent on the thickness of the joint. This implies a Q factor of

$$ Q = {1 \over d_b} \left( d_h + {l \over 10} \right) ~~\text{when}~~ D_J \gt 3 d_h ~~\text{and}~~ l \le 8 d_h $$

(17)

A plot of Q for various thicknesses and D_J/d_h ratios is shown in Figure 4. The data was generated assuming a 5/8" diameter bolt, d, with a bolt head diameter of 15/16" (1.5 time the bolt diameter), d_h. From this data we can see there is a large variation in Q depending on the thickness of the joint relative to the bolt diameter and the joint diameter (i.e. how much material is being clamped) relative to the bolt diameter.

Figure 4. Q factors for Various Geometries Using the Bickford Method

5.2 Shigley's Frustum Approach

Shigley [16] used a similar methodology but made a different assumption about the shape of the stress field to better correlate with experimental data. In this method, the stiffness in a layer is obtained by assuming the stress field looks like a frustum of a hollow cone (See Figure 5).

By assuming a 1D (i.e. axial) compression (see Shigley [16] for the complete derivation), the stiffness of a layer can be computed as

$$ k_i = { \pi ~E ~d_b \tan(\alpha) \over \ln \left({ (2 l \tan(\alpha) + d_h - d_b)(d_h + d_b) \over (2 l \tan(\alpha) + d_h + d_b)(d_h - d_b) }\right) } $$

(18)

Various angles, α, have been used. 45 degrees is often used but this often over estimates the clamping stiffness. Shigley states that typically the angle to use should be between 25 and 33 degrees and in general recommends 30 degrees (this is assuming a washer is used). There are two obvious examples when this falls apart. The first is for the case when there is not enough material for the frustum to exist (e.g., a bolt hole very near an edge of a plate). The second case is for very thick clamping areas. For this case, the shape of the actual stress distribution looks more like a barrel and the shape assumed by Shigley is inappropriate.

There are a number of subtleties that must be noted based on the assumptions in this method. First, there must be 'symmetric' frustums across the entire joint regardless of the number of materials (otherwise static equilibrium would not be met). The value of D used for a given layer must take into account the frustum of the previous layer and not just the bolt or washer diameter. The actual value of d_h that really should be used is the start of the stress frustum and not the diameter of the bolt head and/or washer. Due to flexibility in the bolt or washer, the correct value of d_h will be less than the bolt head (or washer) diameter and the degree to which it is less depends on the relative stiffness of the materials involved. If the bolt is in a threaded hole, the starting point for the frustum at the threaded end should be at the bolt threads and this is typically assumed to be at the midpoint of the engaged threads and d_h is typically used instead of d_b. This is not strictly correct but is accurate enough with all the other assumptions built into the method. The actual point of where one frustum begins and the other ends must be computed for each layer.

It should be pointed out that Shigley [16] suggests that the work of Wileman [17] is the preferred method (when it is applicable) to the frustum approach presented here. It, and extensions to it, will be presented in the next section. It is assumed by the authors that this is because it is a simpler method not because it is necessarily more accurate. As will be shown, the results for the frustum approach and the Wileman approach produce very similar results for joints with only one material.

5.3 FEA Based Empirical Approaches

Wileman [17] used finite element analysis to determine the clamped material stiffness for two "plates" made of the same material. It is based on a standard spring stiffness model for the overall joint that was previously discussed. The results of this work produce a clamped material stiffness for commercial metals of

$$ k_m = 0.78952 ~E ~d_b ~e^{ 0.62914 ~d_b / l } $$

(19)

where E is the Young's modulus of the material, d_b is the diameter of the bolt and l is the thickness of the clamped materials (i.e. the two "plates").

Musto [10] extended this approach to two materials by introducing two new variables

$$ E_{eff} = { 1 \over {1 \over E_{ms} } + n \left( {1 \over E_{ls}} - {1 \over E_{ms}} \right) } $$

(20)

$$ n = { l_{ls} \over l } $$

(21)

where ms denotes the 'more stiff' material and ls denotes the 'less stiff' material. He then proposed the clamped material stiffness to be

$$ k_m = E_{eff} ~d_b \left[ m \left( {d_b \over l} \right) + b \right] $$

(22)

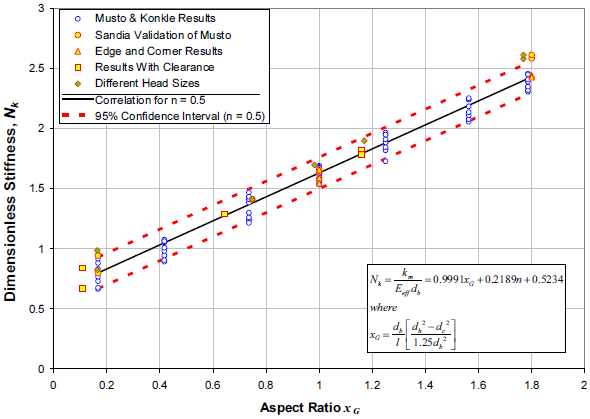
and computed valued of m and b based on different materials stiffness ratios between materials and ratios of bolt diameter to clamped material length. Durbin, Morrow, and Petti [9] analyzed Musto's results and concluded a general purpose equation across materials and geometries could be written. They also extended the work to address clearances, edge effects and variable bolt head diameters. They determined the clamped material stiffness including accounting for clearances, edge effects and variable bolt head diameters can be written as

$$ k_m = E_{eff} ~d_b ~( 0.9991 ~x_G + 0.2189 ~n + 0.5234 ) $$

(23)

where

$$ x_G = { d_b \over l } \left({ d_h^2 - d_c^2 \over 1.25 ~d_b^2 }\right) $$

(24)

This relationship is valid for aspect ratios of bolt diameter to length of clamped material between 0.167 and 1.786, and is still restricted to two materials. The correlation has a standard error of 0.065. Figure 6 shows the correlation and how it matches to the finite element data.

Durbin et al. [9] compared this equation to the one derived for the Q-factor method and noted the only unknown between the two equations is Q. They implemented an iterative solve for Q and incorporated that into an updated spreadsheet based on the original work of Pulling [13].

5.4 Edge Effects

Durbin, Morrow and Petti [6] examined boundary effects of bolted joints when the bolt head diameter (or washer) is 1.5 times larger than the bolt diameter and in the restricted d_b/l range of 0.167 to 1.786. They followed the methodology of Musto [10] that was described in the previous section and looked at both edge effects and corner effects. They concluded that there is not significant degradation of the joint until the edge or corner effect is within 1.5 bolt diameters of the hole. As such, the methods described in the previous section should be applicable to most bolted joints.

5.5 Comparison of the Analytic Methods

To get a quantitative comparison of the various analytic method relative to one another, consider the case of 5/8" bolt with a bolt head diameter of 15/16" (1.5 times the bolt diameter) clamping two "plates" of the same material. In this case, it is possible to solve for an equivalent Q for each method. We will only consider cases where there is significant clamped materials around the bolt (i.e. the surrounding joint contains material to at least three times the bolt diameter). This data is shown in Figure 7.

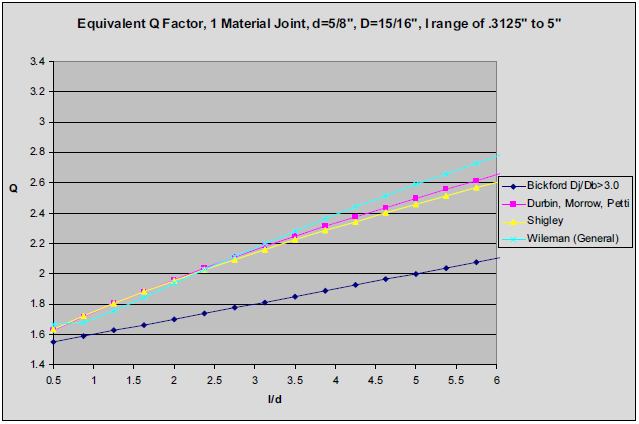
Figure 7. Comparison of Equivalent Q-Factors for the Various Methods with One Material

As expected, the Wileman [17] and Morrow [9] methods produce similar results since Morrow's fit is based on extensions to Wileman's work. The differences are likely due to the fact that Morrow's data covers multiple materials in addition to various geometries and Wilemans's data is for a single material. Shigley's method [16] is also similar to the other two methods. The divergence in the methods occurs as the clamped material gets thick compared to the bolt diameter. Bickford's [4] method is dramatically different than the other 2 and in comparison will produce much lower clamped material stiffness. It appears it is overly conservative and will not be considered further in this document.

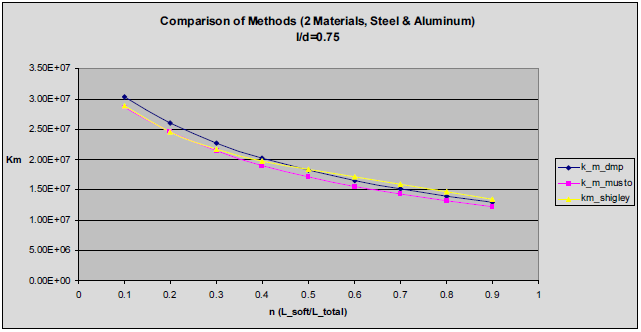
The next comparison that can be made is using two materials for Shigley's method [16] and the extension of Wileman [17] by Musto [10] and then Morrow [9]. Again consider the case of 5/8" bolt with a bolt head diameter of 15/16" (1.5 times the bolt diameter) clamping two "plates". In this case, one "plate" will be made from steel and the other plate from aluminum. The relative amount of each material will be varied from 10% to 90% of the total joint thickness. Figure 8 shows the results for an l/d_b ratio of 0.75 (this represents a "thin" clamped joint) and Figure 9 shows the results for an l/d_b ratio of 5.0 (this represents a "thick" clamped joint). As can be seen in Figure 8 the methods produce very similar results for "thin" clamped joints. As can be seen in Figure 9, the methods are very similar for "thick" clamped joints when there is a significant fraction of soft material (i.e. aluminum in this case), but significant differences when there is a significant fraction of stiff material (i.e. steel in this case). Although not shown, this significant difference begins at roughly an l/d_b ratio of about 2.0.

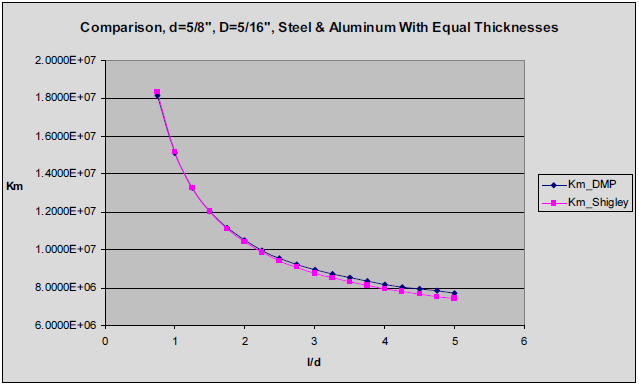
In Figure 9 it can be noted that the results look similar for equal thicknesses of the two materials (i.e. at n = 0.5) at the bounds. Figure 10 shows the results for n = 0.5 across the range of l/d ratios. The methods produce very similar results. The trends of Morrow [9] seem to be more physically intuitive and are backed up by finite element analysis. The Shigley method must use 3 frustums for n ≠ 0.5 because the 'knee' is not at the interface. The use of 3 frustums introduces some error as discussed previously. Based on this, it is recommended to use the Morrow method whenever only 2 layers of material are being clamped and the l/d_b ratio is within their recommended bounds. Otherwise, the Shigley method is recommended. A follow on to this work will be to extend the Morrow method to more than two materials and verify the results.

Figure 8. Comparison of Member Stiffness for Two Materials and l/d=0.75

Figure 9. Comparison of Member Stiffness for Two Materials and l/d=5.0

Figure 10. Comparison of Shigley & Durbin With Two Equal Thickness Materials (n=0.5)

5.6 Recommendations for Analytic Approaches

All of the analytic or empirical approaches presented in this chapter make assumptions and are quite good in many cases but none applies in every case. Nonetheless, these methods constitute the first tool available to an engineer looking at bolted joints. In general, it is recommended to use these types of approaches and evaluate if a higher fidelity analysis is required.

In summary, three approaches to calculating joint stiffness have been presented. The first is a method based on an assumed cylindrical stress field. Bickford's [4] and Pulling's [13] work is based on this assumption. The positives of this method include the overall simplicity of the application of the method, the simplicity with which the effect of clearance holes can be accounted for, and that an extension to including bending to the factor of safety calculations may be included (although they should be used with great care since the underlying assumptions are based on beam theory accurately portraying the joint). The down side of this method is that the accuracy is highly dependent on the choice of Q (or the area). The axial stiffness computed by this method is proportional to Q² and the bending stiffness computed by this method is proportional to Q⁴. As such, small errors in Q become large errors in the member stiffness. The data shown in Figure 7 indicates that Q can reasonably vary from 1.6 to 2.6 depending on the geometry. The second method, from Shigley [16], is based on an assumption the stress field can be represented as a hollow frustum of a cone. While there are subtleties to applying the method, it has been used successfully since the 1960's for designing and analyzing bolted joints and it is general enough to apply to any axisymmetric geometry (although the accuracy is unknown at best or questionable at worst for anything but simple geometries). The third method is based on using finite element analysis of bolted joints and fitting the results with empirical equations. The work of Wileman [17], Musto [10] and Morrow [9] are all based on this method and each is an extension of the previous work. In the latest form, this method has been shown to be applicable to most commercial metals (including Steel, Aluminum, Brass and Titanium) and a wide range of geometries including two-material joints. The method is the easiest to apply and has been 'verified' since it was based on finite element calculations. The down side is that it is only applicable for two layer joints and only applies in certain ranges of geometries (although it should be noted the range is relatively broad and likely to cover most engineering applications).

The ultimate choice is of course left up to the engineer designing and/or analyzing the joint. Any of the methods can be used successfully if the engineer is aware of the assumptions and limitations and applies the theory correctly. Based on the pros and cons of each method, it is recommended that the empirical method of Morrow [9] be used as the preferred method when it is applicable. In cases, where it is not, it is recommended that the hollow frustum approach of Shigley [16] be used. The reasons for recommending the DMP method are 1) it matches very well with finite element analysis and Shigley's frustum approach for standard cases, 2) it doesn't have the subtleties and the unknown accuracy for differing materials with different thickness (but matches extremely well for identical thicknesses where Shigley is known to be accurate) and 3) it is the easiest to apply and gives the same results in cases where both are equally applicable. It is planned for follow on work to extend the work of Morrow [9] to cases of more than two materials and perhaps to expand the range of geometries that it is applicable to. For cases where a high degree of accuracy is required, the geometries and/or materials don't match the assumptions of these analytic methods, the loading is complicated, or the margins are very small, it is recommend that a finite element analysis be performed on the joint.

6 Partitioning Axial Tensile Load Between the Joint and the Bolt

Now that an estimate for the bolt stiffness, k_b, and the clamped material stiffness, k_m, has been obtained, we can examine how an externally applied tensile load is partitioned between them. An applied axial load, F, will produce a displacement, δ. Part of the load will be taken up by the bolt, F_b, and part will be taken up by the clamped material, F_m. We know the bolt and the clamped material act as springs in parallel so we can solve for the total displacement (assuming the joint is not loaded to the point where the material is no longer clamped which is complete failure of the joint) as

$$ \delta = { F \over k_b + k_m } $$

(25)

The stiffness constant, C, of the joint is defined to be the ratio of the load taken by the bolt to that of the joint as a whole and can be computed as

$$ C = { k_b \over k_b + k_m } $$

(26)

The part of externally applied load that is taken up by the bolt can be computed as

F_b = CF = k_bδ

(27)

and the load in the clamped material can be computed as

F_m = (1 − C)F = k_mδ

(28)

7 Thermal Loads

Thermal effects are important in many bolted applications. A change in temperature can cause an increase or a decrease in the preload of the bolt. This can lead to over-stressing the bolt or reducing the clamping load and therefore reducing the frictional capacity of the joint. This section outlines how to account for the thermal loads. It should be noted that this analysis requires the stiffness of each material so it can not be used for the FEA based empirical approaches that just define the total member stiffness.

It should be recalled that the analytic/empirical approaches are based on the assumption that the joint is considered to be two springs in parallel (one representing the bolt and one representing the clamped material that is made from a set of springs in series representing the different layers of material). That assumption is valid throughout this section as well given that the expansion (or contraction) is only axial (i.e. there is either no radial expansion or there is sufficient clearance to prevent interference due to the thermal expansion). An unconstrained object will expand due to a change in temperature as

ΔL_{unconstrained} = α_L L ΔT

(29)

where ΔL is the change in length due to thermal effects, αL is the coefficient of thermal expansion, L is the length, and ΔT is the change in temperature. A bolted joint is constrained so the actual change in length will be the natural extension plus some amount (which can be zero) due to the constraints. This can be written as

ΔL = ΔL_{unconstrained} + ΔL_constrained

(30)

Where ΔL is the total extension (i.e. the extension that would be physically measured) and ΔL_constrained is the extension caused by the constraint. ΔL_constrained is the extension that will result in load being generated in the joint. From the springs in parallel assumptions, we know the total extension of the bolt equals the total extension of the layers which can be written as

$$ \Delta L_{bolt} = \sum_{i} \Delta L_{layer_i} $$

(31)

From static equilibrium, the force in the bolt is equal and opposite to the force in each layer which can be written as

F_bolt = −F_{layer_i}

(32)

The force can be related to the constrained displacement for each layer (and similarly for the bolt) as

F_i = k_i ΔL_{constrained_i}

(33)

If we have N layers of clamped materials, we have 2*N+2 unknowns (N+1 forces and N+1 extensions, the +1 is for the bolt). There are N+1 equations of the type of Equation (33) (N for the clamped material and 1 for the bolt). There are N equations of the type of Equation (32) (one for each layer). Equation (31) is one additional equation. This gives 2*N+2 equations in 2*N+2 unknowns which is easily solvable. This set of equations yields the additional loads due to the thermal effects.

The NASA method [11] for incorporating thermal loads into the factor of safety calculations will be adopted here. The thermal load that increases the tensile load will be added to the maximum preload when computing the factor of safety of the bolt. The thermal load that reduces the tensile load will be subtracted from the minimum preload when computing the factor of safety for joint opening. These are of course the conservative assumptions.

8 Thread Tear Out

It is preferable to have the bolt break rather than strip out the threads if a joint is going to fail [12]. All of the equations in this section are taken from [12] except where specifically noted.

8.1 Equal Tensile Strength Internal and External Threads

For the case of equal tensile strengths of the internal and external threads, the length of engagement of the threads to prevent the threads stripping out should be more than

$$ L_e = { 2 ~A_t \over \pi ~d_{mt} ~[ 0.5 + n ~(d_{bmp} - d_{mt}) ~\tan(30^{\circ}) ] } $$

(34)

where L_e is the minimum length of engagement, A_t is the tensile stress area of the screw head (given below), n is the number of threads per inch, d_mt is the maximum minor diameter of the internal threads, and d_bmp is the minimum pitch diameter of the external threads. For unified screw threads and steels of up to 100 ksi ultimate tensile strength, the Machinery's Handbook recommends using

$$ A_t = {\pi \over 4} \left( d_b - {0.9743 \over n} \right)^2 $$

(35)

and for steels over 100 ksi ultimate tensile strength recommends using

$$ A_t = {\pi \over 4} \left( {d_{bmp} \over 2} - {0.16238 \over n} \right)^2 $$

(36)

For M-form metric threads, Bickford [5] recommends using

$$ A_t = {\pi \over 4} ( d_b - 0.9382 \cdot P)^2 $$

(37)

where P is the thread pitch.

Bickford [5] uses these same equations for the case where the internal threads are stronger than the external, and this is the practice recommended here.

8.2 Higher Tensile Strength Bolt

To determine if the internal threads will strip out before the bolt break, first compute the factor J as

$$ J = { A_s ~S_{y,ET} \over A_n ~S_{u,IT} } $$

(38)

where S_y,ET is the tensile strength of the external thread material and S_u,IT is the tensile strength of the internal material and the shear areas of the external and internal threads are computed as

A_s = π L_e d_mt [ 0.5 + n (d_bmp − d_mt ) tan(30°) ]

(39)

A_n = π L_e d_bmm [ 0.5 + n tan (30°) (d_bmm − d_t ) ]

(40)

where d_bmm is the minimum major diameter of the external threads, d_i is the maximum pitch diameter of the internal threads.

The minimum length of engagement of the threads, K_e, to ensure the internal threads are not stripped out can be computed as

K_e = J L_e

(41)

where L_e is computed in the previous section.

9 Additional Issues

There are a number of additional issues that will be discussed here. There is not currently a sufficiently general approach to all of these issues so the engineer must use his/her judgment on them. The issues include bending loads, torsional loads, and fatigue.

9.1 Bending Loads

Bending loads can come from two primary sources. The first primary source of bending loads is direct bending applied to the bolt during the preload phase due to geometric effects. These can include off center holes, deformation due to the preload causing bending (e.g., pipe flanges bending due to the gap between them when preloaded), or other geometric effects. These loads can be significant and should be accounted for but there is no general approach to handle the cases so the engineer must determine how to account for them and to ensure the design meets all the criteria when considering these loads. The second primary source of bending loads is a bending load applied to the structure that must be transmitted through the bolted joint. The classic example would be a pipe with a bending load applied to it. The bending load will be primarily seen by the bolts as axial load (tensile on one side and compression on the other). In the long term, it is planned to look at pressure vessel design codes where this issue is addressed to see if they can be applied in a general way. Until then, the engineer must use their judgment and come up with an axial load that can be applied directly.

9.2 Torsional Loads

In general, it is highly recommended that any torsional load be carried through shear by having multiple bolts and/or shear pins rather than by a single bolt. If this is done, a hand calculation of the shear load on the bolts can done and that load added directly into the loads on the bolt (it is desirable to have the shear load taken by frictional capacity in which case the actual load the bolt would see is zero). Preliminary analysis indicates a joint with a single threaded fastener can resist torque loads on the order of the applied preload torque. No additional guidance is provided for the case of a single bolt resisting a moment since it is so undesirable.

9.3 Fatigue

Fatigue is a known issue for bolted joints subjected to cyclic loading. This is not a mature area and further investigation is needed in the future. A brief overview of the various options for assessing fatigue life are provided here but ultimately the engineer must use his/her judgment when assessing fatigue life of bolted joints.

For constant amplitude cyclic loading, there are multiple theories to define stress-life curves in terms of the alternating stress, σ_alt, the mean stress, σ_mean, the endurance limit, S_e, and the true fracture stress, σ_fracture [3]. These include Soderberg,

$$ {\sigma_{alt} \over S_e} + {\sigma_{mean} \over S_y} = 1 $$

(42)

Goodman,

$$ {\sigma_{alt} \over S_e} + {\sigma_{mean} \over S_u} = 1 $$

(43)

Gerber,

$$ {\sigma_{alt} \over S_e} + \left( {\sigma_{mean} \over S_u} \right)^2 = 1 $$

(44)

and Morrow

$$ {\sigma_{alt} \over S_e} + {\sigma_{mean} \over S_{fracture}} = 1 $$

(45)

Bannantine [3] makes the following generalizations about these relationships for the general area of fatigue NOT specific to bolted joints. The Soderberg method is very conservative and seldom used. Actual test data tend to fall between the Goodman and Gerber curves. For hard steels (i.e., brittle) where the ultimate strength approaches the true fracture stress, the Morrow and Goodman lines are essentially the same. For ductile steels, the Morrow line predicts less sensitivity to mean stress. For cases with a small mean stress in relationship to the alternating stress, there is little difference in the theories. For cases with a small alternating stress compared to the mean stress, there is little data.

Lindeburg [7] suggests using the Goodman theory multiplied by an appropriate stress concentration factor based on the stress concentration at the beginning of the threaded section. For rolled threads, he suggests an average stress concentration factor of 2.2 for SAE grades 0 to 2 and a factor of 3.0 for SAE grades 4 to 8. He also notes that stress concentration factors for cut threads are much higher.

For variable amplitude loading, Miner's rule can be used to estimate fatigue life [1]. Miner's Rule is a linear theory for damage accumulation (non-linear theories exist but will not be discussed here). It is a linear theory because it is assumed that sum of the ratios of cycles at a given amplitude to the fatigue life at that amplitude can be summed to get the total effect of the variable loading, and it is independent of the order of the loading. Bannantine [3] notes that Miner's rule can be non-conservative for two level tests where the initial level is a high amplitude and the second level is a low amplitude. Bannantine [3] also notes that tests using random histories with several stress levels show very good correlation with Miner's rule. Miner's rule for determining failure due to fatigue can be written simply in the form

$$ \sum {n_i \over N_i} \ge 1 $$

(46)

where ni is the number of cycles at the ith stress amplitude level and Ni is the number of cycles to failure at the ith stress amplitude. Alternatively, the part will not fracture due to variable amplitude loading if

$$ \sum {n_i \over N_i} \lt 1 $$

(47)

The complication of using Miner's rule for real parts, is determining the amplitudes and the number of cycles. For real loads, this is non-trivial and multiple methods have been recommended. A discussion of them is beyond the scope of this document and the reader is referred to a reference on fatigue such as Bannantine [3]. One method recommended in this reference will be explicitly noted because it comes from an ASTM standard and is called Rainflow counting [2]. No effort has been made to ensure this is still 'state of the art' so an interested reader may want to pursue a literature search. It is planned to update this document in the future, and this is one area that needs additional work.

10 Finite Element Approaches

If the analytic/empirical approaches above are not applicable or additional accuracy is required, then the recommended approach is a finite element analysis of the joint. Roach [14] outlined a two phase finite element approach (linear and non-linear) that is adopted here.

10.1 Linear Elastic Analysis

The first step would be a linear elastic finite element calculation. A linear analysis allows for accurate geometric representation and loading effects and limited contact effect can also be incorporated. There are many packages that can be used and the exact modeling approach depends on both the package and what is needed from the analysis.

10.2 Non-Linear Analysis

Using a non-linear finite element analysis can be very expensive and requires significant expertise. Using it implies the need to have a very accurate solution due to small margins, designing into the non-linear regime, and/or other non-traditional design spaces. The nonlinearities that can be modeled include geometric non-linearities, frictional sliding contact, and material non-linearities (including plastic yielding) so a high degree of accuracy can be obtained if appropriately used. Due to the complexity of this type of analysis, it should only be done by experienced analysts.

11 Combining Loads and Factor of Safety Calculations

When considering factors (or margins) of safety for bolted joints, it must be realized that part of the load on the joint (the preload and resulting clamping forces) should NOT be scaled by the applied loads to account for the factors of safety, they are fixed. As such, how to consider factors of safety must be considered.

The method used for combining loads and accounting for factors of safety used by NASA [11] and recommended by Bickford [5] will be adopted here. A ratio of applied stress, factoring in the required factors of safety, to allowable stress (this applies to both yield and ultimate strengths) is defined independently for the tensile load (R_t) and the shear load (R_s) as

$$ R_T = { (F_{preload.max} + F_{thermal} + FOS \cdot C \cdot F) / A_T \over S_{tensile} } $$

(48)

$$ R_s = { FOS \cdot \tau_{applied} \over S_{shear} } $$

(49)

where F_preload.max is the maximum applied preload before considering thermal effects, F is the applied tensile load, A_T is the cross sectional tensile area, FOS is the required factor of safety, S_tensile is the tensile strength (applies for both yield and ultimate strength), τ_applied is the applied shear stress, and S_shear is the shear strength (applies for both yield and ultimate strength).

The bolt meets the factor of safety for the combined load if the following inequality is met

R_T^X + R_S^Y ≤ 1

(50)

where X and Y are chosen dependent on how much conservatism is desired. NASA [11] chose X = 2 and Y = 3 and Bickford [5] states these are the accepted aerospace values. The most conservative choice would be X = 1 and Y = 1 (which Bickford recommends for cases where weight is not a concern). This is overly conservative and in general the NASA values should be sufficient.

A margin of safety based on Equation (50) can be written as

MOS = 1 − (R_T^X + R_S^Y)

(51)

Because the required factors of safety have already been incorporated, MOS only needs to be positive for the bolt to meet the required factor of safety for combined loading. These equations apply for both yield and ultimate strength factor of safety calculations. It should be noted that for a purely tensile load case (i.e., no shear so R_s = 0), Equation (51) has a margin of safety of zero when the joint exactly meets the factor of safety requirement regardless of the choice of X. As such, it can be used for both combined and tensile only in cases to judge if the joint meets the factor of safety requirements.

These calculations require knowing the tensile yield and ultimate strength, which is easy to obtain, as well as the shear yield and ultimate strengths, which are not generally known. Bickford [5] suggests that in general the shear ultimate strength for steels is between 0.55 (for stainless steels and aluminum) to 0.60 (for carbon steels) times the tensile ultimate strength.

12 Conclusions

This report provides a guideline for designing and analyzing bolted joints. The primary focus of this guide has been on analytic/empirical methods for analyzing axial and thermal loads. For the cases where these methods are applicable, this guide should be sufficient as an initial design and analysis guideline. A Mathcad worksheet is described in Appendix B for performing the calculations and an example problem is shown in Appendix C. For cases where the methods are not applicable, high levels of accuracy are needed, or the margins computed here are very small, the engineer should resort to finite element analyses. The methods of Pulling [13], and the associated Excel spreadsheet, can still be used and reasonable results obtained, but it is important to understand the theory, the limitations, and the deficiencies in it. Using it incorrectly can result in very large errors (due to the fact that Q varies dramatically depending on the joint and materials and any errors in it are at best squared, amplifying the error).

There are many issues where little if any useful information has been provided and additional work is needed. These include better guidelines for choosing a pre-computed nut factor or using a method to compute a more accurate nut factor, bending effects (both globally applied that result in axial loads on the bolt and local bending on the bolt due to geometric effects such as bolting a pipe flange that has a gap between materials), fatigue analysis, extending the DMP method [9] to more than two materials and how to include thermal effects with it, and guidelines on designing bolted joints to carry shear load (including frictional capacity, shear pins, shear load applied to the bolts, etc.)

References

Avallone, E. A. & T. Baumeister III, Marks Standard Handbook for Mechanical Engineers, 9^th Edition, McGraw Hill Book Company, NY, 1987.
American Society for Testing and Materials, Annual Book of ASTM Standards, Section 3: Metals Test Methods and Analytical Procedures, Vol. 03.01-Metals-Mechanical Testing; Elevated and Low-Temperature Tests, ASTM, Philadelphia, 1986, pp. 836-848.
Bannantine, J. A., J. J. Comer and J. L. Handrock, Fundamentals of Metal Fatigue Analysis, Prentice Hall Inc, New Jersey, 1990.
Bickford, J. H., An Introduction to the Design and Behavior of Bolted Joints, Second Edition, Marcel Dekker, NY, 1990.
Bickford, J. H. and S. Nassar, Editors, Handbook of Bolts and Bolted Joints, Marcel Dekker, NY, 1998.
Durbin, Samuel, Charles Morrow, and Jason Petti, "Review of Bolted Joints near Material Edges", Internal Sandia Memo, 2007.
Lindeburg, M. R., Mechanical Engineering Reference Manual for the PE Exam, 11^th Edition, Professional Publications, Belmont, CA, 2001.
Miller, Keith, private conversations, 2007.
Morrow, Charles and Samuel Durbin, "Review of the Scale Factor, Q, Approach to Bolted Joint Design", Internal Sandia Memo, 2007.
Musto, J. C. and N. R. Konkle, "Computation of Member Stiffness in the Design of Bolted Joints", ASME J. Mech. Des., November, 2006, 127, pp. 1357-1360.
National Aeronautics and Space Administration, "Space Shuttle: Criteria for Preloaded Bolts", NSTS 080307 Revision A, July 6, 1998.
Oberg, E., F. D. Jones, L. H. Holbrook, and H. H. Ryffel, Machinery's Handbook, 27^th Edition, Industrial Press Inc, NY, 2004
Pulling, E. M., S. Brooks, C. Fulcher, K. Miller, Guideline for Bolt Failure Margins of Safety Calculations, Internal Sandia Report, December 7, 2005.
Roach, R. A, Working Draft of "Design & Analysis Guidelines for Satellite Fasteners & Flexures", 2007.
Shigley, J. E., C. R. Mischke, and T. H. Brown, Jr., Standard Handbook of Machine Design, 7^th Edition, McGraw-Hill Book Company, NY, 2004.
Shigley, J. E., C. R. Mischke, and R. G. Budynas, Mechanical Engineering Design, 7^th Ed., McGraw-Hill Book Company, NY, 2004.
Wileman, J., M. Choudhury, and I. Green, "Computation of Member Stiffness in Bolted Connections," ASME J. Mech Des., December, 1991, 113, pp. 432-437.

Appendix A: Nut Factors

There are multiple methods for computing a nut factor. Two of those methods are presented here.

An analytic expression for the nut factor, K [12], can be written as

$$ K = {1 \over 2 d_b} \left( {P \over \pi} + \mu_t d_2 \sec \alpha' + \mu_B D_B \right) $$

(52)

where P is the screw thread pitch, μ_t is the coefficient of friction between the threads, μ_B is the coefficient of friction between the bearing surfaces, D_B is the equivalent diameter of the friction torque bearing surfaces and can be computed when the contact area is circular as

$$ D_B = {2 \over 3} \left({ D_0^{~3} - D_i^{~3} \over D_0^{~2} - D_i^{~2} }\right) $$

(53)

and

α' = tan^-1(tanβ cosα)

(54)

where β is the thread half angle, and α is the thread helix, or lead, angle.

NASA [11] allows using either pre-computed nut factors or computing the preload (without considering the uncertainties here but which must be accounted for later) as

$$ F_P = { T \over R_o \left( \tan \alpha + { \mu_t \over \cos \beta } \right) + R_e \mu_b } $$

(55)

where R_o is the effective radius of the thread forces (approximately half the basic pitch diameter of external threads), α is the thread lead angle, μ_t is the coefficient of friction between the threads, β is the thread half angle, μ_b is the coefficient of friction between the nut and the bearing surface, and R_e is defined as

$$ R_e = { R_o + R_i \over 2 } $$

(56)

where R_o is the outer radius of the torqued element (nut of head) and R_i is the inner radius of the torqued element. This is equivalent to a nut factor of

$$ K_{NASA} = {1 \over d_b} \left[ R_t \left( \tan \alpha + { \mu_t \over \cos \beta } \right) + R_e \mu_b \right] $$

(57)

It is not recommended to use these equations. They are here to give some perspective to what goes into the nut factor. The Machinery's Handbook [12] has precomputed data for various sizes of bolts, threads and friction coefficients. A table of nut factors was given in Table 4. These analytic methods seem to produce nut factors that are much larger than the experimentally accepted values. Additional work will be done to understand the differences in a future revision of this document.